题目内容
 如图,D是等边△ABC的边AB上的一个动点(D与A、B不重合),以CD为一边向上作等边△EDC,连接AE.
如图,D是等边△ABC的边AB上的一个动点(D与A、B不重合),以CD为一边向上作等边△EDC,连接AE.
(1)说明四边形ABCE是梯形;
(2)当D在AB边上的什么位置时,四边形ABCE是直角梯形(直接写出结论);
(3)在(2)的条件下,当AB=4时,求梯形的面积.
解:(1)∵△ABC与△DEC都为等边三角形,
∴AB=BC=AC,DE=EC=CD,∠ACB=∠DCE=60°,
∴∠DCE-∠ACD=∠ACB-∠ACD,即∠ACE=∠BCD,
在△ACE和△BCD中,
 ,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠B=60°,
∴AE∥BC,又AB与EC不平行,
∴四边形ABCE为梯形;
(2)当CD⊥AB时,四边形ABCE是直角梯形,理由为:
∵CD⊥AB,
∴∠BDC=90°,
∵△ACE≌△BCD,
∴∠AEC=90°,
∴四边形ABCE为直角梯形;
(3)在(2)条件下,四边形ABCE为直角梯形,
∴∠BCE=90°,又∠ACB=60°,
∴∠ACE=30°,
在Rt△ACE中,AC=AB=BC=4,∠ACE=30°,
∴AE= AC=2,EC=
AC=2,EC= =2
=2 ,
,
则S梯形ABCE= (AE+BC)•EC=
(AE+BC)•EC= ×(2+4)×2
×(2+4)×2 =6
=6 .
.
分析:(1)由三角形ABC与三角形DEC都为等边三角形,根据等边三角形的三边相等,三角相等都为60°,得到AC=BC,CE=CD,∠ACB=∠DCE=60°,利用等式的性质得到∠ACE=∠BCD,利用SAS得出三角形ACE与三角形BCD全等,由全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到AE与BC平行,而AB与EC不平行,可得出四边形ABCE为梯形;
(2)当CD与AB垂直时,四边形ABCE为直角梯形,当CD与AB垂直时,得到∠BDC为直角,由全等三角形的对应角相等得到∠AEC=∠BDC=90°,即可确定出梯形ABCE为直角梯形;
(3)在(2)条件下,四边形ABCE为直角梯形,且∠AEC=90°,此时∠ACE为30°,由AB=AC=BC=4,在直角三角形ACE中,利用直角三角形中30°所对的直角边等于斜边的一半求出AE的长,再利用勾股定理求出EC的长,利用梯形的面积公式即可求出梯形ABCE的面积.
点评:此题考查了等边三角形的判定与性质,全等三角形的判定与性质,含30°直角三角形的性质,以及勾股定理,熟练掌握判定与性质是解本题的关键.
∴AB=BC=AC,DE=EC=CD,∠ACB=∠DCE=60°,
∴∠DCE-∠ACD=∠ACB-∠ACD,即∠ACE=∠BCD,
在△ACE和△BCD中,
 ,
,∴△ACE≌△BCD(SAS),
∴∠CAE=∠B=60°,
∴AE∥BC,又AB与EC不平行,
∴四边形ABCE为梯形;
(2)当CD⊥AB时,四边形ABCE是直角梯形,理由为:
∵CD⊥AB,
∴∠BDC=90°,
∵△ACE≌△BCD,
∴∠AEC=90°,
∴四边形ABCE为直角梯形;
(3)在(2)条件下,四边形ABCE为直角梯形,
∴∠BCE=90°,又∠ACB=60°,
∴∠ACE=30°,
在Rt△ACE中,AC=AB=BC=4,∠ACE=30°,
∴AE=
 AC=2,EC=
AC=2,EC= =2
=2 ,
,则S梯形ABCE=
 (AE+BC)•EC=
(AE+BC)•EC= ×(2+4)×2
×(2+4)×2 =6
=6 .
.分析:(1)由三角形ABC与三角形DEC都为等边三角形,根据等边三角形的三边相等,三角相等都为60°,得到AC=BC,CE=CD,∠ACB=∠DCE=60°,利用等式的性质得到∠ACE=∠BCD,利用SAS得出三角形ACE与三角形BCD全等,由全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到AE与BC平行,而AB与EC不平行,可得出四边形ABCE为梯形;
(2)当CD与AB垂直时,四边形ABCE为直角梯形,当CD与AB垂直时,得到∠BDC为直角,由全等三角形的对应角相等得到∠AEC=∠BDC=90°,即可确定出梯形ABCE为直角梯形;
(3)在(2)条件下,四边形ABCE为直角梯形,且∠AEC=90°,此时∠ACE为30°,由AB=AC=BC=4,在直角三角形ACE中,利用直角三角形中30°所对的直角边等于斜边的一半求出AE的长,再利用勾股定理求出EC的长,利用梯形的面积公式即可求出梯形ABCE的面积.
点评:此题考查了等边三角形的判定与性质,全等三角形的判定与性质,含30°直角三角形的性质,以及勾股定理,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.
如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.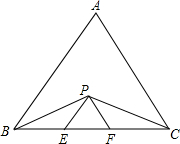 如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.
如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.