题目内容
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当 是腰长为5的等腰三角形时,点P的坐标为 。
是腰长为5的等腰三角形时,点P的坐标为 。

 是腰长为5的等腰三角形时,点P的坐标为 。
是腰长为5的等腰三角形时,点P的坐标为 。
(2,4)或(3,4)或(8,4)。
当△ODP是腰长为5的等腰三角形时,有三种情况,需要分类讨论:
(1)如图①所示,PD=OD=5,点P在点D的左侧,

过点P作PE⊥x轴于点E,则PE=4。
在Rt△PDE中,由勾股定理得:
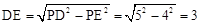 ,
,
∴OE=OD-DE=5-3=2。
∴此时点P坐标为(2,4)。
(2)如图②所示,PD=OD=5,点P在点D的右侧,

过点P作PE⊥x轴于点E,则PE=4。
在Rt△PDE中,由勾股定理得:
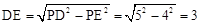
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)。
(3)如图③所示,OP=OD=5。

过点P作PE⊥x轴于点E,则PE=4。
在Rt△POE中,由勾股定理得: ,
,
∴此时点P坐标为(3,4)。
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4)。
(当OP=PD时,OP不能满足为5的条件)
(1)如图①所示,PD=OD=5,点P在点D的左侧,

过点P作PE⊥x轴于点E,则PE=4。
在Rt△PDE中,由勾股定理得:
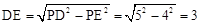 ,
,∴OE=OD-DE=5-3=2。
∴此时点P坐标为(2,4)。
(2)如图②所示,PD=OD=5,点P在点D的右侧,

过点P作PE⊥x轴于点E,则PE=4。
在Rt△PDE中,由勾股定理得:
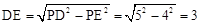
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)。
(3)如图③所示,OP=OD=5。

过点P作PE⊥x轴于点E,则PE=4。
在Rt△POE中,由勾股定理得:
 ,
,∴此时点P坐标为(3,4)。
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4)。
(当OP=PD时,OP不能满足为5的条件)

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目


 轴上,且关于
轴上,且关于 轴对称时,A点坐标为( )
轴对称时,A点坐标为( ) ),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,且则点M的坐标是( , ) .
),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,且则点M的坐标是( , ) .
 一定不在
一定不在 ,将线段AB经过平移后得到线段
,将线段AB经过平移后得到线段 ,若点A的对应点为
,若点A的对应点为 ,则点B的对应点
,则点B的对应点 的坐标是 .
的坐标是 .
