Question

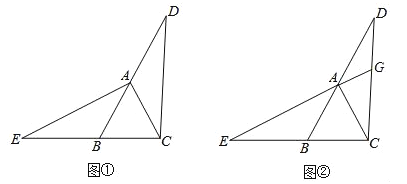
【题目】如图①．在△ABC中，AB＝AC，∠ABC＝60°，延长BA至点D，延长CB至点E，使BE＝AD，连接CD、AE．

（1）求证：△ACE≌△CBD；

（2）如图②，延长EA交CD于点G，则∠CGE的度数是　 　度．

Answer 1

【答案】（1）证明见解析；（2）60°．

【解析】

(1)根据等边三角形的判定与性质可知，AC＝CB＝AB，∠ABC＝∠ACB＝60°，因为BE＝AD，所以CE＝BD，然后根据全等三角形的判定定理，即可证明结论成立；

(2)根据全等三角形的性质即可求出∠CGE的度数.

（1）∵AB＝AC，∠ABC＝60°，∴△ABC是等边三角形，∴BC＝AC，∠ACB＝∠ABC．

∵BE＝AD，∴BE+BC＝AD+AB，即CE＝BD．在△ACE和△CBD中，，∴△ACE≌△CBD（SAS）；

（2）如图2中，∵△ABC是等边三角形，由（1）可知△ACE≌△CBD，∴∠E＝∠D．

∵∠BAE＝∠DAG，∴∠E+∠BAE＝∠D+∠DAG，∴∠CGE＝∠ABC．

∵∠ABC＝60°，∴∠CGE＝60°．