题目内容
【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
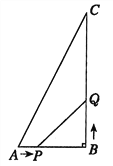
(1)当![]() 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
【答案】(1)8;(2)当![]() =3时,
=3时,![]() 有最小值27
有最小值27![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据直角三角形的面积公式和路程=速度×时间进行求解即可;
(2)四边形APQC的面积=△ABC的面积﹣△PBQ的面积,再根据配方法即可求解;
(3)分两种情况讨论:![]() 和
和![]() ,求出对应的t即可.
,求出对应的t即可.
试题解析:(1)当![]() 时,AP=2,BQ=4,PB=4,∴
时,AP=2,BQ=4,PB=4,∴![]() =
=![]() (
(![]() );
);
(2)∵AP=![]() ,BQ=
,BQ=![]() ,PB=
,PB=![]() ,∴
,∴![]() =
= ![]()
=![]() ,∴当
,∴当![]() =3时,
=3时,![]() 有最小值27
有最小值27![]() ;
;
(3)∵△PQB、△ABC是直角三角形,∴由![]() ,即
,即![]() ,解得
,解得![]() ,由
,由![]() ,即
,即![]() ,解得
,解得![]() ,∴当
,∴当![]() 或
或![]() 时,△PQB与△ABC相似.
时,△PQB与△ABC相似.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】下表是初二年级50名同龄女生身高数据:
身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
(1)根据下表的分组方法进行数据整理,补全频数分布表:
(2)根据分布表画出频数分布直方图.
(3)观察频数分布表和频数分布直方图回答问题:为了参加广播操比赛,老师打算从以上50名女生中挑选30名队员。为了让参赛队员的身高比较整齐,老师应该选择身高在什么范围内的同学呢?请写出答案并简述理由.