题目内容
若0°＜θ＜90°，且|sin2θ-
|+（cosθ-
）2=0，则tanθ的值等于
- A.
- B.
- C.
- D.
B
分析：根据非负数的性质得到sin2θ-=0，cosθ-=0，再根据特殊角的三角函数解答．
解答：由0°＜θ＜90°，且|sin2θ-|+（cosθ-）2=0，
得：sin2θ-=0，cosθ-=0，
∴sinθ=，cosθ=，
∴tanθ=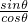
=．
故选B．
点评：本题利用了两个非负数的和等于0，则这两个非负数均为0，还利用了tanθ=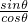来求值．
分析：根据非负数的性质得到sin2θ-
=0，cosθ-=0，再根据特殊角的三角函数解答．解答：由0°＜θ＜90°，且|sin2θ-
|+（cosθ-）2=0，得：sin2θ-
=0，cosθ-=0，∴sinθ=
，cosθ=，∴tanθ=
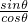=．故选B．
点评：本题利用了两个非负数的和等于0，则这两个非负数均为0，还利用了tanθ=
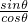来求值． 
练习册系列答案
备战中考寒假系列答案
相关题目
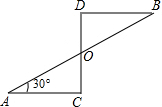（2013•南充模拟）如图是一个以O为对称中心的中心对称图形，若∠A=30°，∠C=90°，AC=1，则AB的长为（ ）
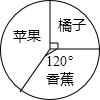（2009•保定一模）某水果店购进苹果、橘子、香蕉三种水果，它们所占比例如图所示，若购进的橘子为90千克，那么，购进的苹果为
