题目内容
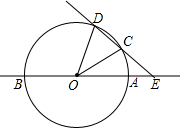如图，直线AB经过⊙O的圆心，与⊙O相交于A、B两点，点C在⊙O上，且∠AOC=30度．点E是直线AB上的一个动点（与点O不重合），直线EC交⊙O于D，则使DE=DO的点E共有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析：作出图形，根据画图可知应分E在AB的延长线上、在BA的延长线上、在线段AB上，三种情况来解决．
解答：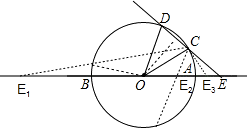
解：
如图所示，点E的位置有3个．当是E1时，∠CE1O=10°；
当是E2时，则∠CE20=110°；
当是E3时，则∠CE3O=50°．
故选C．
点评：此题根据等腰三角形的性质和三角形的内角和定理即可得到三种情况．
分析：作出图形，根据画图可知应分E在AB的延长线上、在BA的延长线上、在线段AB上，三种情况来解决．
解答：
解：如图所示，点E的位置有3个．当是E1时，∠CE1O=10°；
当是E2时，则∠CE20=110°；
当是E3时，则∠CE3O=50°．
故选C．
点评：此题根据等腰三角形的性质和三角形的内角和定理即可得到三种情况．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
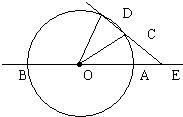7、如图，直线AB经过⊙O的圆心，与⊙O相交于A、B两点，点C在⊙O上，且∠AOC=30度．点E是直线AB上的一个动点（与点O不重合），直线EC交⊙O于D，则使DE=DO的点E共有（ ）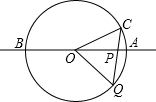
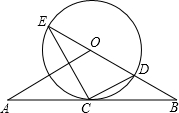如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，连接EC、CD．
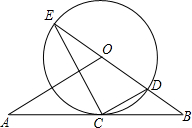CD．
合），过点P分别向x轴、y轴作垂线，垂足分别为C、D．设OC=x，四边形OCPD的面积为S．