题目内容
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,直线OB交⊙O于点E,D,连接EC,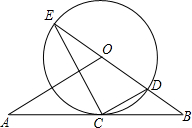 CD.
CD.(1)试判断直线AB与⊙O的位置关系,并加以证明;
(2)求证:BC2=BD•BE;
(3)若tanE=
| 1 | 2 |
分析:(1)根据题目给的OA=OB,CA=CB的条件,很容易证明直线AB与⊙O的位置关系是相切.
(2)连接AC,根据题目所给的条件去证明△BCD∽△BEC,问题可解.
(3)设BC的长是x,因为△BCD∽△BEC,根据相似三角形的对应边成比例,可求出OB=OA=2x-3,根据勾股定理可求解.
(2)连接AC,根据题目所给的条件去证明△BCD∽△BEC,问题可解.
(3)设BC的长是x,因为△BCD∽△BEC,根据相似三角形的对应边成比例,可求出OB=OA=2x-3,根据勾股定理可求解.
解答: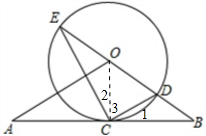 解:(1)AB与⊙O相切,连接OC,
解:(1)AB与⊙O相切,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB,
∵点C在⊙O上,
∴AB与⊙O相切
(2)连接OC,∵OC⊥AB,
∴∠OCB=90°即∠1+∠3=90°,
又∵DE为⊙O的直径,
∴∠ECD=90°即∠2+∠3=90°,
∴∠1=∠2,
∵OE=OC,
∴∠E=∠2,
∴∠1=∠E,
∵∠B=∠B,
∴△BCD∽△BEC,
∴
=
,
∴BC2=BD•BE;
(3)∵tanE=
,∠ECD=90°,
∴
=
,
∵⊙O的半径为3,
∴OC=OE=3,
∵△BCD∽△BEC,
∴
=
,设BC=x,
∴
=
,
∴OB=2x-3,
∵∠OCB=90°,
∴OC2+BC2=OB2,
∴9+x2=(2x-3)2,
∴x1=0(舍去),x2=4,
∴OA=OB=5.
 解:(1)AB与⊙O相切,连接OC,
解:(1)AB与⊙O相切,连接OC,∵OA=OB,CA=CB,
∴OC⊥AB,
∵点C在⊙O上,
∴AB与⊙O相切
(2)连接OC,∵OC⊥AB,
∴∠OCB=90°即∠1+∠3=90°,
又∵DE为⊙O的直径,
∴∠ECD=90°即∠2+∠3=90°,
∴∠1=∠2,
∵OE=OC,
∴∠E=∠2,
∴∠1=∠E,
∵∠B=∠B,
∴△BCD∽△BEC,
∴
| BC |
| BE |
| BD |
| BC |
∴BC2=BD•BE;
(3)∵tanE=
| 1 |
| 2 |
∴
| CD |
| EC |
| 1 |
| 2 |
∵⊙O的半径为3,
∴OC=OE=3,
∵△BCD∽△BEC,
∴
| BC |
| BE |
| CD |
| EC |
∴
| x |
| OB+3 |
| 1 |
| 2 |
∴OB=2x-3,
∵∠OCB=90°,
∴OC2+BC2=OB2,
∴9+x2=(2x-3)2,
∴x1=0(舍去),x2=4,
∴OA=OB=5.
点评:本题考查了相似三角形的判定和性质,勾股定理以及切线的判定和性质,关键是熟记这些性质定理和判定定理.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
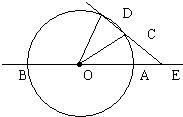 7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )
7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )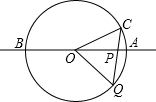
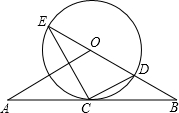 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD. 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.