题目内容
(2012•顺义区二模)如图,直线AB经过第一象限,分别与x轴、y轴交于A、B两点,P为线段AB上任意一点(不与A、B重 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
(1)若已知A(4,0),B(0,6),求S与x之间的函数关系式;
(2)若已知A(a,0),B(0,b),且当x=
时,S有最大值
,求直线AB的解析式;
(3)在(2)的条件下,在直线AB上有一点M,且点M到x轴、y轴的距离相等,点N在过M点的反比例函数图象上,且△OAN是直角三角形,求点N的坐标.
 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.(1)若已知A(4,0),B(0,6),求S与x之间的函数关系式;
(2)若已知A(a,0),B(0,b),且当x=
| 3 |
| 4 |
| 9 |
| 8 |
(3)在(2)的条件下,在直线AB上有一点M,且点M到x轴、y轴的距离相等,点N在过M点的反比例函数图象上,且△OAN是直角三角形,求点N的坐标.
分析:(1)利用待定系数法求出直线AB的解析式,表示出点P的坐标,利用举行的面积公式就可以求出S与x之间的函数关系式.
(2)设直线AB的解析式,表示出点P的坐标及矩形的面积,将x=
时,S有最大值
代入解析式就可以求出系数的值.从而求出直线的解析式.
(3)设出点M的坐标由题意可以代入解析式分类讨论求出M的坐标,然后由M的坐标求出反比例的解析式,最后由△OAN是直角三角形就可以求出点N的坐标.
(2)设直线AB的解析式,表示出点P的坐标及矩形的面积,将x=
| 3 |
| 4 |
| 9 |
| 8 |
(3)设出点M的坐标由题意可以代入解析式分类讨论求出M的坐标,然后由M的坐标求出反比例的解析式,最后由△OAN是直角三角形就可以求出点N的坐标.
解答:解:(1)设直线AB的解析式为y=kx+b,
由A(4,0),B(0,6),得
解得
∴直线AB的解析式为y=-
x+6.
∵OC=x,∴P(x,-
x+6).
∴S=x(-
x+6).
即S=-
x2+6x(0<x<4).
(2)设直线AB的解析式为y=mx+n,
∵OC=x,
∴P(x,mx+n).
∴S=mx2+nx.
∵当x=
时,S有最大值
,
∴
解得
∴直线AB的解析式为y=-2x+3.
∴A(
,0),B(0,3).
即a=
,b=3.
(3)设点M的坐标为(xM,yM),
由点M在(2)中的直线AB上,
∴yM=-2xM+3.
∵点M到x轴、y轴的距离相等,
∴xM=yM或xM=-yM.
当xM=yM时,M点的坐标为(1,1).
过M点的反比例函数的解析式为y=
.
∵点N在y=
的图象上,OA在x轴上,且△OAN是直角三角形,
∴点N的坐标为(
,
).
当xM=-yM时,M点的坐标为(3,-3),
过M点的反比例函数的解析式为y=-
.
∵点N在y=-
的图象上,OA在x轴上,且△OAN是直角三角形,
∴点N的坐标为(
,-6).
综上,点N的坐标为(
,
)或(
,-6).
由A(4,0),B(0,6),得
|
|
∴直线AB的解析式为y=-
| 3 |
| 2 |
∵OC=x,∴P(x,-
| 3 |
| 2 |
∴S=x(-
| 3 |
| 2 |
即S=-
| 3 |
| 2 |
(2)设直线AB的解析式为y=mx+n,
∵OC=x,
∴P(x,mx+n).
∴S=mx2+nx.
∵当x=
| 3 |
| 4 |
| 9 |
| 8 |
∴
|
|
∴直线AB的解析式为y=-2x+3.
∴A(
| 3 |
| 2 |
即a=
| 3 |
| 2 |
(3)设点M的坐标为(xM,yM),
由点M在(2)中的直线AB上,
∴yM=-2xM+3.
∵点M到x轴、y轴的距离相等,
∴xM=yM或xM=-yM.
当xM=yM时,M点的坐标为(1,1).
过M点的反比例函数的解析式为y=
| 1 |
| x |
∵点N在y=
| 1 |
| x |
∴点N的坐标为(
| 3 |
| 2 |
| 2 |
| 3 |
当xM=-yM时,M点的坐标为(3,-3),
过M点的反比例函数的解析式为y=-
| 9 |
| x |
∵点N在y=-
| 9 |
| x |
∴点N的坐标为(
| 3 |
| 2 |
综上,点N的坐标为(
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题试一道一次函数的综合试题,考查了待定系数法求直线函数的解析式及反比例函数的解析式,二次函数的解析式,直角三角形的性质的运用.解答中注意点M到x轴、y轴的距离相等的点有两个,不要漏掉.

练习册系列答案
相关题目
 (2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )
(2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )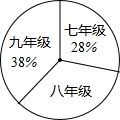 图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:
图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题: