题目内容
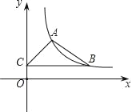
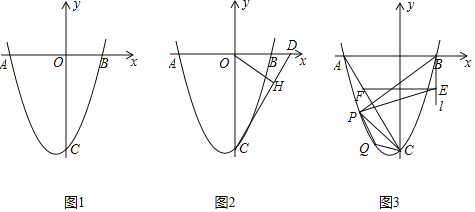
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
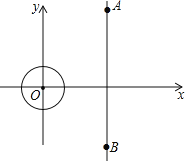
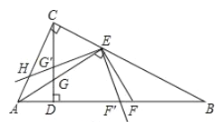
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
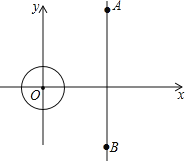
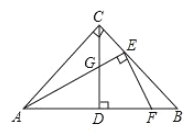
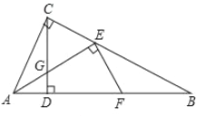
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
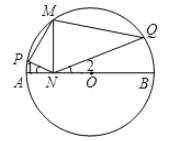
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
【答案】(1)y=x2+x﹣6;(2)OH+![]() HC的最小值为3
HC的最小值为3![]() ;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
【解析】
(1)把交点坐标代入抛物线交点式表达式,即可求解;
(2)作点O关于直线BC的对称点O′,过点O′作O′G⊥y轴交DC与点H、交y轴与点G,在图示的位置时,OH+![]() HC为最小值,即可求解;
HC为最小值,即可求解;
(3)①PE=CF,则PEcosβ=SFcosβ,即:PE=FS,即可求解;②求出HP所在的直线表达式与二次函数联立,求得交点即可.
解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2)=(x+3)(x﹣2)=x2+x﹣6,
抛物线的表达式为:y=x2+x﹣6…①,
(2)作点O关于直线DC的对称点O′交CD于点M,过点O′作O′G⊥y轴交DC与点H、交y轴与点G,
∵OD=2![]() ,OC=6,则∠OCD=30°,∴GH=
,OC=6,则∠OCD=30°,∴GH=![]() HC,
HC,
在图示的位置时,OH+![]() HC=GH+OH,此时为最小值,长度为GO′,
HC=GH+OH,此时为最小值,长度为GO′,
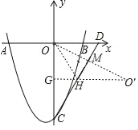
∵O′O⊥DC,∴∠OO′H=∠OCD=30°,
∴OM=![]() OC=3=
OC=3=![]() OO′,
OO′,
在Rt△OO′G中,GO′=OO′cos∠OO′G=6cos30°=3![]() ,
,
即:OH+![]() HC的最小值为3
HC的最小值为3![]() ;
;
(3)①设点P的坐标为(m,n),n=m2+m﹣6,
直线AC表达式的k值为﹣2,则直线PE表达式的k值为![]() ,
,
设直线PE的表达式为:y=![]() x+b,
x+b,
将点P坐标代入上式并解得:b=n﹣![]() m,
m,
则点E的坐标为(2,1+n﹣![]() m),点F的坐标为(
m),点F的坐标为(![]() m﹣
m﹣![]() n﹣
n﹣![]() ,1+n﹣
,1+n﹣![]() m),
m),
过点P作x轴的平行线交直线l于点M,过点F作y轴平行线交过C点作x轴的平行线于点S,
∵AC⊥PE,∴∠EPM=∠SFC=β,
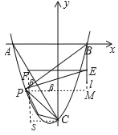
∵PE=CF,则PEcosβ=SFcosβ,即:PE=FS,
∴1+n﹣![]() m+6=2﹣m,即:2m2+3m﹣2=0,
m+6=2﹣m,即:2m2+3m﹣2=0,
解得:m=![]() 或﹣2(舍去m=
或﹣2(舍去m=![]() ),
),
故点P坐标为(﹣2,﹣4),
点E坐标为(2,﹣2);
②过点P作x轴的平行线交直线l于点M、交y轴于点R,作EN⊥PB于点N,
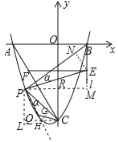
则:PM=4=BM=4,EM=BM=2,
则PE=![]() ,EN=BEsin∠NBE=2×sin45°=
,EN=BEsin∠NBE=2×sin45°=![]() ,
,
设:∠QPC=∠BPE=α,
则sin∠BPE=![]() =
=![]() =sinα,则tanα=
=sinα,则tanα=![]() ,
,
过点P作y轴的平行线交过C点与x轴的平行线于点L,延长PQ交CL于点H,过点H作HG⊥PC,
则:PL=PR=RC=CL=2,即四边形PRCL为正方形,
∴∠PCH=45°,设:GH=GC=m,
PG=![]() =3m,PC=PG+GC=4m=2
=3m,PC=PG+GC=4m=2![]() ,则m=
,则m=![]() ,
,
CH=![]() m=1,即点H坐标为(﹣1,﹣6),
m=1,即点H坐标为(﹣1,﹣6),
则HP所在的直线表达式为:y=﹣2x﹣8…②,
①②联立并解得:x=﹣1或﹣2(x=﹣2和点P重合,舍去),
故点Q的坐标为(﹣1,﹣6).
故答案为:(1)y=x2+x﹣6;(2)OH+![]() HC的最小值为3
HC的最小值为3![]() ;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).
;(3)①点P坐标为(﹣2,﹣4);②点Q的坐标为(﹣1,﹣6).

 名校课堂系列答案
名校课堂系列答案