题目内容
【题目】![]() 光在反射时,光束的路径可用图(1)来表示,
光在反射时,光束的路径可用图(1)来表示,![]() 叫做入射光线,
叫做入射光线,![]() 叫做反射光线,从入射点
叫做反射光线,从入射点![]() 引出的一条垂直于镜面
引出的一条垂直于镜面![]() 的射线
的射线![]() 叫做法线,
叫做法线,![]() 与
与![]() 的夹角
的夹角![]() 叫入射角,
叫入射角,![]() 与
与![]() 的夹角
的夹角![]() 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得:![]() .则图(1)中
.则图(1)中![]() 与
与![]() 的数量关系是:____________理由:___________;
的数量关系是:____________理由:___________;

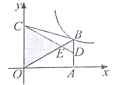
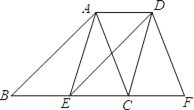
![]() 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”
生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”![]() 射入到平面镜
射入到平面镜![]() 上、被
上、被![]() 反射到平面镜
反射到平面镜![]() 上,又被平面镜
上,又被平面镜![]() 反射后得到反射光线
反射后得到反射光线![]() .
.

(1)若反射光线![]() 沿着入射光线
沿着入射光线![]() 的方向反射回去,即
的方向反射回去,即![]() ,且
,且![]() ,则
,则![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)猜想:当![]() ______
______![]() 时,任何射到平面镜
时,任何射到平面镜![]() 上的光线
上的光线![]() 经过平面镜
经过平面镜![]() 和
和![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.
【答案】![]()
![]() ,等角的余角相等;
,等角的余角相等;![]() (1)70,90;(2)90,见解析.
(1)70,90;(2)90,见解析.
【解析】
1.新知探究:利用等角的余角相等解决问题即可.
2.问题解决:(1)想办法求出∠BCO,∠CBO即可解决问题.
(2)当∠O=90°时,AB∥CD.设∠ABE=x.求出∠ABC,∠BCD即可判断.
1.新知探究:∵α+∠1=90°,β+∠2=90°,α=β,
∴∠1=∠2(等角的余角相等),
故答案为∠1=∠2,等角的余角相等.
2.问题解决:(1)由题意:∠ABE=∠CBO=35°,
∴∠ABC=110°,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=70°,
∴∠BCO=∠DCF=55°,
∴∠O=180°-35°-55°=90°,
故答案为70°,90°.
(2)当∠O=90°中时,AB∥CD.设∠ABE=x.
则∠ABE=∠CBO=x,∠BCO=∠DCF=90°-x,
∴∠ABC=180°-2x,∠BCD=180°-2(90°-2x)=2x,
∴∠ABC+∠BCD=180°,
∴AB∥CD.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案