题目内容
【题目】快车与慢车分别从甲、乙两地同时相向出发,匀速而行,快车到达乙地后停留![]() ,然后原路按原速返回,此时,快车比慢车晚
,然后原路按原速返回,此时,快车比慢车晚![]() 到达甲地,快、慢两车距各自出发地的路程
到达甲地,快、慢两车距各自出发地的路程![]() 与所用的时
与所用的时![]() 的关系如图所示.
的关系如图所示.
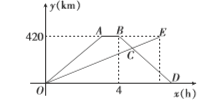
(1)甲、乙两地之间的路程为____________![]() .
.
(2)求![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.
(3)当快、慢两车相距![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)420;(2)![]() 解析式为
解析式为![]() ;(3)
;(3)![]() 的值为1.1或2.9或5.3.
的值为1.1或2.9或5.3.
【解析】
(1)根据图象即可得出答案;
(2)先求出D点的坐标,然后利用待定系数法即可求出BD的解析式及x的取值范围;
(3)从图象可知,分三种情况:①当快、慢两车没有相遇时;②当快、慢两车相遇后,但快车还未到乙地时;③当快车从乙地返回甲地时,分别进行讨论即可.
解:(1)根据图象可知,甲、乙两地之间的路程为420km.
(2)由图可知快车的速度为![]() ,
,
∴快车7小时回到甲地,
∴![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
设![]() 解析式为
解析式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴![]() 解析式为
解析式为![]() .
.
(3)由题意知,慢车6小时到达甲地,
则慢车的速度为![]() ,则OE的解析式为
,则OE的解析式为![]()
两车相距![]() 分三种情况:
分三种情况:
①当快、慢两车没有相遇时,![]() ,解得
,解得![]() ;
;
②当快、慢两车相遇后,但快车还未到乙地时,![]() ,解得
,解得![]() ;
;
③当快车从乙地返回甲地时,![]() ,解得
,解得![]() .
.
综上,当快、慢两车相距![]() 时,
时,![]() 的值为1.1或2.9或5.3.
的值为1.1或2.9或5.3.

【题目】某中学举行“中国梦·校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如下图所示:

根据图示信息,整理分析数据如下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(说明:图中虚线部分的间隔距离均相等)
(1)求出表格中![]() 的值;
的值;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.