题目内容
14.等边△ABC的边长为2,点D在射线CB上,点E在射线AC上,AD=AE,∠EDC=15°,则线段CD的长为4.分析 连接DE,由△ABC是等边三角形,得到∠ABC=∠ACB=∠BAC=60°,根据三角形的外角的性质得到∠E=45°,得到∠DAC=90°,根据等腰三角形的性质得到AB=BD=2,于是得到结论.
解答  解:连接DE,
解:连接DE,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∵∠EDC=15°,
∴∠E=45°,
∵AD=AE,
∴∠ADE=∠E=45°,
∴∠DAC=90°,
∴∠ADB=∠BAD=30°,
∴AB=BD=2,
∴CD=BD+BC=4,
故答案为:4.
点评 本题考查了的等边三角形的性质,直角三角形的判定和性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
6.下列各式计算正确的是( )
| A. | -8-2×6=(-8-2)×6 | B. | 2÷$\frac{4}{3}$×$\frac{3}{4}$=2÷($\frac{4}{3}$×$\frac{3}{4}$) | ||
| C. | (-1)2004+(-1)2005=1+(-1)=0 | D. | -(-3 2)=-9 |
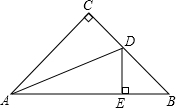 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,则△DBE的周长等于10cm.
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,则△DBE的周长等于10cm.



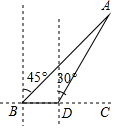 如图,海中有一个小岛A,轮船在B点测得小岛A在北偏东45°方向上,轮船由西向东航行20海里到达D点,这时测得小岛A在北偏东30°方向上,求此时轮船与小岛A的距离AD是多少海里?(结果精确到0.1)参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
如图,海中有一个小岛A,轮船在B点测得小岛A在北偏东45°方向上,轮船由西向东航行20海里到达D点,这时测得小岛A在北偏东30°方向上,求此时轮船与小岛A的距离AD是多少海里?(结果精确到0.1)参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.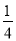 )﹣1+(﹣2)2×50﹣(
)﹣1+(﹣2)2×50﹣(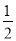 )﹣2;
)﹣2; 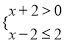 的解集是( )
的解集是( )