题目内容
【题目】如图,AB与CD交于点O,OM为射线.
(1)写出∠BOD的对顶角;
(2)写出∠BOD与∠COM的邻补角;
(3)已知∠AOC=70°,∠BOM=80°,求∠DOM和∠AOM的度数.

【答案】(1)∠AOC;(2)∠BOD的邻补角为∠BOC和∠DOA;∠COM的邻补角为∠MOD;(3) 100°
【解析】
(1) 如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,根据对顶角的定义即可求解,
(2)·两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角,根据邻补角的定义即可求解,
(3)由∠AOC=70°,根据对顶角的性质可得出: ∠BOD=70°,再根据∠BOM=80°,可得∠DOM=∠DOB+∠BOM=70°+80°=150°, ∠COM=180°-∠AOC-∠BOM=180°-70°-80°=30°, ∠AOM=∠AOC+∠COM=70°+30°=100°.
(1)∠BOD的对顶角为∠AOC,
(2)∠BOD的邻补角为∠BOC和∠DOA,∠COM的邻补角为∠MOD,
(3)∵∠AOC=70°,∠BOM=80°,
∴∠BOD=∠AOC=∠70°,∠COM=180°-∠AOC-∠BOM=180°-70°-80°=30°,
∴∠DOM=∠DOB+∠BOM=70°+80°=150°,
∠AOM=∠AOC+∠COM=70°+30°=100°.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
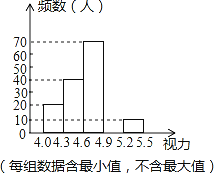
欣语文化快乐暑假沈阳出版社系列答案【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?