题目内容
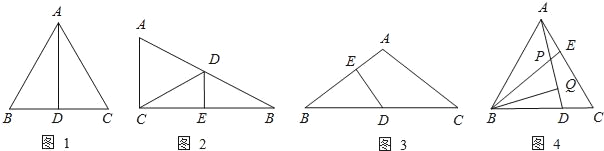
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
【答案】(1)15cm;(2)3:1;(3)BQ=![]() .
.
【解析】整体分析:
(1)由“直角三角形中,30°角所对的直角边等于斜边的一半”求AC的长;(2)连接AD,由“三线合一”得∠BAD=60°,利用直角三角形中的30°角所对的直角边的性质,分别把BE,EA用BD表示;(3)证明△BAE≌△ACD,得∠BPQ=60°,结合勾股定理求解.
解:(1)∵DE是线段BC的垂直平分线,∠ACB=90°,
∴CD=BD,AD=BD.
又∵在△ABC中,∠ACB=90°,∠B=30°,
∴AC=![]() AB,
AB,
∴△ACD的周长=AC+AB=3BD=15cm.
故答案为15cm;
(2)连接AD,如图所示.
∵在△ABC中,AB=AC,∠A=120°,D是BC的中点,
∴∠BAD=60°.
又∵DE⊥AB,
∴∠B=∠ADE=30°,∴BE=![]() BD,EA=
BD,EA=![]() AD,
AD,
∵BD=![]() AD,∴EA=
AD,∴EA=![]() AD=
AD=![]() BD.
BD.
∴BE:EA=![]() BD:
BD: ![]() AD,
AD,
∴BE:AE=3:1.
故答案为3:1.

(3)∵△ABC为等边三角形.
∴AB=AC,∠BAC=∠ACB=60°,
在△BAE和△ACD中,
AE=CD,∠BAC=∠ACB,AB=AC,
∴△BAE≌△ACD(SAS),∴∠ABE=∠CAD.
∵∠BPQ为△ABP外角,
∴∠BPQ=∠ABE+∠BAD.∴∠BPQ=∠CAD+∠BAD=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=30°,∴BP=2PQ=2,∴PQ=1,
∴BQ=![]() =
=![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?




