题目内容
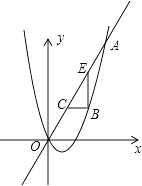
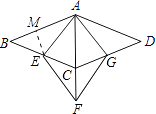
【题目】如图，四边形ABCD与四边形AEFG都是菱形，其中点C在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，则 
= ． 
【答案】
【解析】解：∵∠BAD=135°，∠EAG=75°，四边形ABCD与四边形AEFG都是菱形， ∴∠B=180°﹣∠BAD=45°，∠BAE=∠BAC﹣∠EAC=30°，
过点E作EM⊥AB于点M，设EM=x，
在Rt△AEM中，AE=2EM=2x，AM= 
x，
在Rt△BEM中，BM=x，
则 
= 
= ．
所以答案是： ．
【考点精析】本题主要考查了等腰直角三角形和含30度角的直角三角形的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一定时间后，测试出这种植物高度的增长情况，部分数据如表：
温度t/℃ | ﹣4 | ﹣2 | 0 | 1 | 4 |
植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
科学家经过猜想、推测出l与t之间是二次函数关系．由此可以推测最适合这种植物生长的温度为℃．
