题目内容
如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段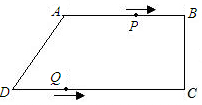 DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.
DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
分析:(1)过点A作AM⊥CD于M,根据勾股定理,可以求出DM=6所以DC=16.
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图示,由题可得:BP=10-3t,DQ=2t,所以可以列出方程10-3t=2t,解得t=2,此时,BP=DQ=4,CQ=12,在△CBQ中,根据勾股定理,求出BQ即可.
(3)此题要分三种情况进行讨论:即①当点P在线段AB上,②当点P在线段BC上,③当点P在线段CD上,根据三种情况点的位置,可以确定t的值.
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图示,由题可得:BP=10-3t,DQ=2t,所以可以列出方程10-3t=2t,解得t=2,此时,BP=DQ=4,CQ=12,在△CBQ中,根据勾股定理,求出BQ即可.
(3)此题要分三种情况进行讨论:即①当点P在线段AB上,②当点P在线段BC上,③当点P在线段CD上,根据三种情况点的位置,可以确定t的值.
解答: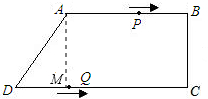 解:(1)过点A作AM⊥CD于M,
解:(1)过点A作AM⊥CD于M,
根据勾股定理,AD=10,AM=BC=8,
∴DM=
=6,
∴CD=16;
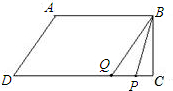
(2)当四边形PBQD为平行四边形时,
点P在AB上,点Q在DC上,如图,
由题知:BP=10-3t,DQ=2t
∴10-3t=2t,解得t=2
此时,BP=DQ=4,CQ=12
∴BQ=
=4
∴四边形PBQD的周长=2(BP+BQ)=8+8
;
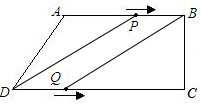
(3)①当点P在线段AB上时,即0≤t≤
时,如图
S△BPQ=
BP•BC=
(10-3t)×8=20
∴t=
.
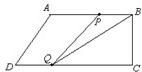
②当点P在线段BC上时,即
<t≤6时,如图
BP=3t-10,CQ=16-2t
∴S△BPQ=
BP•CQ=
(3t-10)×(16-2t)=20
化简得:3t2-34t+100=0,△=-44<0,所以方程无实数解.
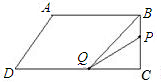
③当点P在线段CD上时,
若点P在Q的右侧,即6≤t≤
,
则有PQ=34-5t
S△⊆BPQ=
(34-5t)×8=20,
t=
<6,舍去
若点P在Q的左侧,
即
<t≤8,
则有PQ=5t-34,S△BPQ=
(5t-34)×8=20,
t=7.8.
综合得,满足条件的t存在,其值分别为t1=
,t2=7.8.
 解:(1)过点A作AM⊥CD于M,
解:(1)过点A作AM⊥CD于M,根据勾股定理,AD=10,AM=BC=8,
∴DM=
| 102-82 |
∴CD=16;
(2)当四边形PBQD为平行四边形时,
点P在AB上,点Q在DC上,如图,
由题知:BP=10-3t,DQ=2t
∴10-3t=2t,解得t=2
此时,BP=DQ=4,CQ=12
∴BQ=
| 82+122 |
| 13 |
∴四边形PBQD的周长=2(BP+BQ)=8+8
| 13 |

(3)①当点P在线段AB上时,即0≤t≤
| 10 |
| 3 |
S△BPQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴t=
| 5 |
| 3 |

②当点P在线段BC上时,即
| 10 |
| 3 |
BP=3t-10,CQ=16-2t
∴S△BPQ=
| 1 |
| 2 |
| 1 |
| 2 |
化简得:3t2-34t+100=0,△=-44<0,所以方程无实数解.

③当点P在线段CD上时,
若点P在Q的右侧,即6≤t≤
| 34 |
| 5 |
则有PQ=34-5t
S△⊆BPQ=
| 1 |
| 2 |
t=
| 29 |
| 5 |
若点P在Q的左侧,
即
| 34 |
| 5 |
则有PQ=5t-34,S△BPQ=
| 1 |
| 2 |
t=7.8.
综合得,满足条件的t存在,其值分别为t1=
| 5 |
| 3 |

点评:本题是平行四边形中的动点问题,解决问题时,一定要变动为静,将其转化为常见的几何问题,再进行解答.

练习册系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.