题目内容
如图所示，平行四边形ABCD的周长是18cm，对角线AC、BD相交于点O，若△AOD与△AOB的周长差是5cm，则边AB的长是________cm．
2
分析：利用平行四边形的对角线互相平分这一性质，确定已知条件中两三角形周长的差也是平行四边形两邻边边长的差，进而确定平行四边形的边长．
解答：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵△AOD的周长=OA+OD+AD，△AOB的周长=OA+OB+AB，
又∵△AOD与△AOB的周长差是5cm，
∴AD=AB+5，
设AB=x，AD=5+x，
则2（x+5+x）=18，
解得x=2，
即AB=2cm．
故答案为2．
点评：本题是应用平行四边形性质的典型题目，解决此题运用了平行四边形的对边相等和角平分线互相平分这两条性质，题目难度不大．
分析：利用平行四边形的对角线互相平分这一性质，确定已知条件中两三角形周长的差也是平行四边形两邻边边长的差，进而确定平行四边形的边长．
解答：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵△AOD的周长=OA+OD+AD，△AOB的周长=OA+OB+AB，
又∵△AOD与△AOB的周长差是5cm，
∴AD=AB+5，
设AB=x，AD=5+x，
则2（x+5+x）=18，
解得x=2，
即AB=2cm．
故答案为2．
点评：本题是应用平行四边形性质的典型题目，解决此题运用了平行四边形的对边相等和角平分线互相平分这两条性质，题目难度不大．
练习册系列答案
习题精选系列答案
相关题目
17、如图所示，平行四边形ABCD，AD=5，AB=9，点A的坐标为（-3，0），则点C的坐标为
18、如图所示，平行四边形ABCD中，E、F分别在AD、BD上，AE=CF，AF与BE交于点G，CE与DF交于点H，猜想EF与GH间的关系，并证明你的猜想．
45°．设边AB的长为x（单位：米），面积为y（单位：米2）．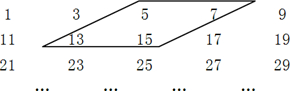
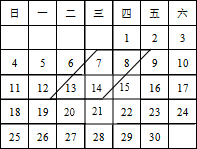（1）用如图所示的平行四边形在日历中圈出了个数，若和为22，则这四个数为