题目内容
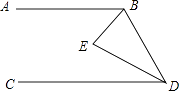
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
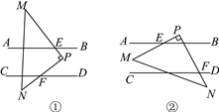
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
【答案】(1)∠PFD+∠AEM=90°;(2)见解析;(3)∠N=45°.
【解析】
(1)如图,由平行线的性质得出∠PFD=∠NPH,∠AEM=∠HPM,即可得出结果;
(2)设PN交AB于点G,由平行线的性质得出∠PFD=∠PGB,再由三角形的外角等于与它不相邻的两个内角的和即可得出结果;
(3)由三角形的外角等于与它不相邻的两个内角的和求出∠PFD=90°+∠PEB=120°,再由平行线的性质得出∠NFO=120°,然后由三角形的内角和定理即可得出结果.
解:(1)如图,过点P作PH∥AB.
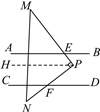
∵AB∥CD,
∴PH∥CD,
∴∠PFD=∠NPH,∠AEM=∠HPM.
∵∠MPN=90°,
∴∠NPH+∠HPM=90°,
∴∠PFD+∠AEM=90°.
(2)证明:设PN交AB于点G.
∵AB∥CD,
∴∠PFD=∠PGB.
∵∠PGB-∠PEB=90°,∠PEB=∠AEM,
∴∠PFD-∠AEM=90°.
(3)由(2)得,∠PFD=90°+∠PEB=120°,
∴∠NFO=120°,
∴∠N=180°-∠DON-∠NFO=45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目