题目内容
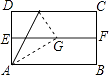
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E, 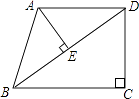
(1)求证:△ABE∽△DCB;
(2)求线段DC的长.
【答案】
(1)证明:
∵AD∥BC,
∴∠ADB=∠DBC,
∵AB=AD,
∴∠ADB=∠ABD,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DCB
(2)解:作AF⊥BC于F,如图,
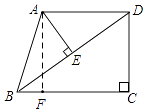
∵AD∥BC,∠C=90°,
∴AFCD是矩形,
∴FC=AD=50,AF=CD,
∴BF=BC﹣FC=64﹣50=14,
∴AF= ![]() =48,
=48,
∴DC=48.
【解析】(1)由AD∥BC得出∠ADB=∠DBC,再由AB=AD得出∠ADB=∠ABD,从而∠ABD=∠DBC,另外AE⊥BD,故∠AEB=∠C=90°,结论显然;(2)作AF⊥BC于F,则AF=CD,FC=AD,算出BF,从而由勾股定理算出AF.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目