题目内容
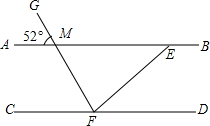 已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
分析:由于AB∥CD,根据两直线平行,同旁内角互补,可知∠BEF=180°-∠EFD;而EF平分∠GFD,由角平分线定义,可知∠EFD=
∠GFD;又根据邻补角定义,可知∠GFD=180°-∠GFC;而由AB∥CD,根据两直线平行,同位角相等,得出∠GFC=∠GMA=52°.
| 1 |
| 2 |
解答:解:∵AB∥CD,(已知)
∴∠GFC=∠GMA.(两直线平行,同位角相等)
∵∠GMA=52°,(已知)
∴∠GFC=52°.(等量代换)
∵CD是直线,(已知)
∴∠GFC+∠GFD=180°.(邻补角定义)
∴∠GFD=180°-52°=128°.(等式性质)
∵EF平分∠GFD,(已知)
∴∠EFD=
∠GFD=64°.(角平分线定义)
∵AB∥CD,(已知)
∴∠BEF+∠EFD=180°.(两直线平行,同旁内角互补)
∴∠BEF=180°-64°=116°.(等式性质)
答:∠BEF=116°.
∴∠GFC=∠GMA.(两直线平行,同位角相等)
∵∠GMA=52°,(已知)
∴∠GFC=52°.(等量代换)
∵CD是直线,(已知)
∴∠GFC+∠GFD=180°.(邻补角定义)
∴∠GFD=180°-52°=128°.(等式性质)
∵EF平分∠GFD,(已知)
∴∠EFD=
| 1 |
| 2 |
∵AB∥CD,(已知)
∴∠BEF+∠EFD=180°.(两直线平行,同旁内角互补)
∴∠BEF=180°-64°=116°.(等式性质)
答:∠BEF=116°.
点评:本题主要考查了平行线的性质、角平分线定义及邻补角定义.

练习册系列答案
相关题目
 10、已知:如图所示,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠ACB相等的角有( )
10、已知:如图所示,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠ACB相等的角有( ) 13、已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=
13、已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=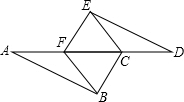 已知:如图所示,AB∥DE,AB=DE,AF=DC.
已知:如图所示,AB∥DE,AB=DE,AF=DC. (2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论:
(2013•孝南区一模)已知,如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交于⊙O于点E,∠BAC=45°,给出以下四个结论: