题目内容
【题目】如图,已知∠A=∠AGE,∠D=∠DGC. 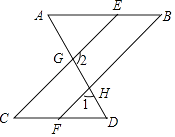
(1)求证:AB∥CD;
(2)若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.
【答案】
(1)证明:∵∠A=∠AGE,∠D=∠DGC,
又∵∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD
(2)证明:∵∠1+∠2=180°,
又∵∠CGD+∠2=180°,
∴∠CGD=∠1,
∴CE∥FB,
∴∠C=∠BFD,∠CEB+∠B=180°.
又∵∠BEC=2∠B+30°,
∴2∠B+30°+∠B=180°,
∴∠B=50°.
又∵AB∥CD,
∴∠B=∠BFD,
∴∠C=∠BFD=∠B=50°
【解析】(1)欲证明AB∥CD,只需推知∠A=∠D即可;(2)利用平行线的判定定理推知CE∥FB,然后由平行线的性质、等量代换推知∴∠C=∠BFD=∠B=50°.
【考点精析】认真审题,首先需要了解平行线的判定(同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目