题目内容
 20、如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
20、如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:证明:∵BD是∠ABC的平分线(
已知
)∴∠ABD=∠DBC(
角平分线定义
)∵ED∥BC(
已知
)∴∠BDE=∠DBC(
两直线平行,内错角相等
)∴
∠ABD=∠BDE
(等量代换
)又∵∠FED=∠BDE(
已知
)∴
EF
∥BD
(内错角相等,两直线平行
)∴∠AEF=∠ABD(
两直线平行,同位角相等
)∴∠AEF=∠DEF(
等量代换
)∴EF是∠AED的平分线(
角平分线定义
)分析:结合角平分线的定义,应用平行线的性质和判定定理可解.
解答:解:证明:∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线定义);
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换);
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠DEF(等量代换),
∴EF是∠AED的平分线(角平分线定义).
∴∠ABD=∠DBC(角平分线定义);
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换);
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠DEF(等量代换),
∴EF是∠AED的平分线(角平分线定义).
点评:主要考查了角平分线的定义,平行线性质和判定等知识点,较为容易.

练习册系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=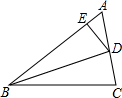 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是