题目内容
 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=45
45
.分析:首先根据△ABD的面积计算出DE的长,再根据角平分线上的点到角两边的距离相等可得DE=DF,然后计算出DF的长,再利用三角形的面积公式计算出△BCD的面积即可.
解答:解:∵S△ABD=36,
∴
•AB•ED=36,
×12×ED=36,
解得:DE=6,
∵BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,
∴DE=DF,
∴DF=6,
∵BC=15,
∴S△BCD=
•CB•DF=
×15×6=45,
故答案为:45.
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:DE=6,
∵BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,
∴DE=DF,
∴DF=6,
∵BC=15,
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:45.
点评:此题主要考查了角平分线的性质,关键是掌握角平分线上的点到角两边的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.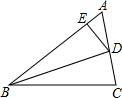 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是