题目内容
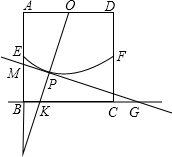 如图,在边长为3的正方形ABCD中,E,F,O分别是AB,CD,AD的中点,以O为圆心,以OE为半径画弧EF.P是
如图,在边长为3的正方形ABCD中,E,F,O分别是AB,CD,AD的中点,以O为圆心,以OE为半径画弧EF.P是 |
| EF |
| BG |
| BM |
| 3 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
分析:此题可以分别从若OP的延长线与射线AB的延长线相交于H与若OP的延长线与射线DC的延长线相交于H去分析,利用切线与正方形的性质,可求得∠H-∠BGM,然后根据三角函数的知识,求得AH的长,继而可得BK的长.注意不要漏解.
解答: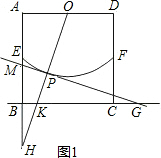 解:(1)若OP的延长线与射线AB的延长线相交,设交点为H.如图1,
解:(1)若OP的延长线与射线AB的延长线相交,设交点为H.如图1,
∵MG与⊙O相切,
∴OK⊥MG.
∴KPG=90°,
∵四边形ABCD是正方形,
∴∠HBK=90°,
∵∠BKH=∠PKG,
∴∠MGB=∠BHK.
∵
=4,
∴tan∠BHK=tan∠BGM=
=
.
∵tan∠BHK=
,
∵O是AD的中点,
∴AO=
,
∴AH=4AO=4×
=6,
∴BH=4BK.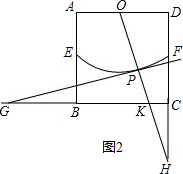
∵AB=3,
∴BH=AH-AB=6-3=3,
∴BK=
×3=
.
(2)若OP的延长线与射线DC的延长线相交,设交点为H.如图2,
同理可求得BK=
.
综上可得:BK=
或
.
故答案为:
或
.
 解:(1)若OP的延长线与射线AB的延长线相交,设交点为H.如图1,
解:(1)若OP的延长线与射线AB的延长线相交,设交点为H.如图1,∵MG与⊙O相切,
∴OK⊥MG.
∴KPG=90°,
∵四边形ABCD是正方形,
∴∠HBK=90°,
∵∠BKH=∠PKG,
∴∠MGB=∠BHK.
∵
| BG |
| BM |
∴tan∠BHK=tan∠BGM=
| BM |
| BG |
| 1 |
| 4 |
∵tan∠BHK=
| AO |
| AH |
∵O是AD的中点,
∴AO=
| 3 |
| 2 |
∴AH=4AO=4×
| 3 |
| 2 |
∴BH=4BK.

∵AB=3,
∴BH=AH-AB=6-3=3,
∴BK=
| 1 |
| 4 |
| 3 |
| 4 |
(2)若OP的延长线与射线DC的延长线相交,设交点为H.如图2,
同理可求得BK=
| 9 |
| 4 |
综上可得:BK=
| 3 |
| 4 |
| 9 |
| 4 |
故答案为:
| 3 |
| 4 |
| 9 |
| 4 |
点评:此题考查了正方形的性质、切线的性质以及三角函数的知识.此题综合性较强,难度较大,解题的关键是根据题意,利用分类讨论思想求解,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
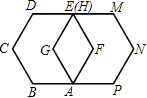 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,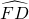 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.