题目内容
【题目】阅读下列材料,解决材料后的问题:
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为:f(x)=![]() ,例如17与16的友好数为f(17,16)=
,例如17与16的友好数为f(17,16)=![]() =
=![]() .
.
材料二:对于实数x,用[x]表示不超过实数x的最大整数,即满足条件[x]≤x<[x]+1,例如:
[﹣1.5]=[﹣1.6]=﹣2,[0]=[0.7]=0,[2.2]=[2.7]=2,……
(1)由材料一知:x2+2与1的“友好数”可以用f(x2+2,1)表示,已知f(x2+2,1)=2,请求出x的值;
(2)已知[![]() a﹣1]=﹣3,请求出实数a的取值范围;
a﹣1]=﹣3,请求出实数a的取值范围;
(3)已知实数x、m满足条件x﹣2[x]=![]() ,且m≥2x+
,且m≥2x+![]() ,请求f(x,m2﹣
,请求f(x,m2﹣![]() m)的最小值.
m)的最小值.
【答案】(1)x=±2;(2)﹣4≤a<﹣2;(3)当m=![]() 时,y有最大值是﹣
时,y有最大值是﹣![]() ,此时f(x,m2﹣
,此时f(x,m2﹣![]() m)有最小值,最小值是﹣
m)有最小值,最小值是﹣![]() .
.
【解析】
(1)由题意得到![]() ,计算即可得到答案;
,计算即可得到答案;
(2)由题意得到![]() ,解不等式即可得到答案;
,解不等式即可得到答案;
(3)先由题意得到![]() ,则
,则![]() ,设
,设![]() ,由题意得到
,由题意得到![]() ,设y=﹣2m2+3m﹣4,根据二次函数的性质即可得到答案.
,设y=﹣2m2+3m﹣4,根据二次函数的性质即可得到答案.
解:(1)∵f(x2+2,1)=2,
∴![]() ,
,
∴x2=4,
∴x=±2;
(2)∵[x]≤x<[x]+1,
∴![]() ,
,
解得﹣4≤a<﹣2;
(3)∵x﹣2[x]=![]() ,
,
∴[x]=![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
又x=2k+![]() ,
,
∴![]() ,
,
∴整数k=﹣3,
∴x=![]() ,
,
又![]() ,
,
∴f(x,m2﹣![]() m),
m),
=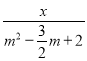 ,
,
= ,
,
=![]() ,
,
设y=﹣2m2+3m﹣4,
则y=﹣2(m![]() )2
)2![]() ,
,
∵﹣2<0,
∴当m=![]() 时,y有最大值是
时,y有最大值是![]() ,此时f(x,m2﹣
,此时f(x,m2﹣![]() m)有最小值,最小值是
m)有最小值,最小值是![]() =﹣
=﹣![]() ,
,
此时最小值为﹣![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目