题目内容
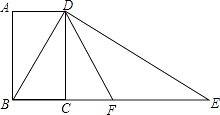
【题目】如图,AD是△ABC的角平分线,∠B=45°,∠ADC=75°,求∠BAC、∠C的度数.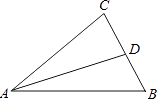
【答案】解:∵∠B=45°,∠ADC=75°,
∴∠BAD=∠ADC﹣∠B=75°﹣45°=30°,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°,
在△ABC中,∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣45°=75°.
【解析】首先根据三角形的一个外角等于与它不相邻的两个内角的和可求出∠BAD,再根据角平分线的定义可得∠BAC=2∠BAD,于是可求得∠BAC的度数,最后在△ABC中利用三角形的内角和为180°可求得∠C的度数.
【考点精析】掌握三角形的内角和外角和三角形的外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目