题目内容
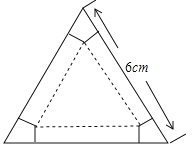
【题目】如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.![]() cm2 B.
cm2 B.![]() cm2 C.
cm2 C.![]() cm2 D.
cm2 D.![]() cm2
cm2
【答案】C.
【解析】
试题分析:∵△ABC为等边三角形,∴∠A=∠B=∠C=60°,AB=BC=AC.∵筝形ADOK≌筝形BEPF≌筝形AGQH,∴AD=BE=BF=CG=CH=AK.∵折叠后是一个三棱柱,∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形,∴∠ADO=∠AKO=90°.连结AO,在Rt△AOD和Rt△AOK中,∵AO=AO,OD=OK,∴Rt△AOD≌Rt△AOK(HL),∴∠OAD=∠OAK=30°.设OD=x,则AO=2x,由勾股定理就可以求出AD=![]() ,∴DE=
,∴DE=![]() ,∴纸盒侧面积=
,∴纸盒侧面积=![]() ==
==![]() ,∴当x=
,∴当x=![]() 时,纸盒侧面积最大为
时,纸盒侧面积最大为![]() .故选C.
.故选C.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目