题目内容
【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA= ![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.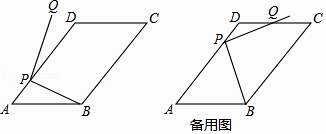
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)
【答案】
(1)
解:如图1中,

①当点Q在平行四边形ABCD内时,∠AP′B=180°﹣∠Q′P′B﹣∠Q′P′D=180°﹣90°﹣10°=80°,
②当点Q在平行四边形ABCD外时,∠APB=180°﹣(∠QPB﹣∠QPD)=180°﹣(90°﹣10°)=100°,
综上所述,当∠DPQ=10°时,∠APB的值为80°或100°
(2)
解:如图2中,连接BQ,作PE⊥AB于E.
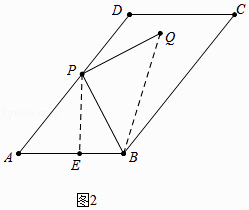
∵tan∠ABP:tanA=3:2,tanA= ![]() ,
,
∴tan∠ABP=2,
在Rt△APE中,tanA= ![]() =
= ![]() ,设PE=4k,则AE=3k,
,设PE=4k,则AE=3k,
在Rt△PBE中,tan∠ABP= ![]() =2,
=2,
∴EB=2k,
∴AB=5k=10,
∴k=2,
∴PE=8,EB=4,
∴PB= ![]() =4
=4 ![]() ,
,
∵△BPQ是等腰直角三角形,
∴BQ= ![]() PB=4
PB=4 ![]()
(3)
解:①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F.则四边形BEPF是矩形.
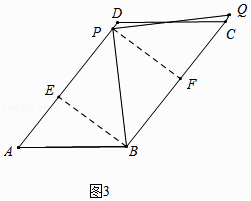
在Rt△AEB中,∵tanA= ![]() =
= ![]() ,∵AB=10,
,∵AB=10,
∴BE=8,AE=6,
∴PF=BE=8,
∵△BPQ是等腰直角三角形,PF⊥BQ,
∴PF=BF=FQ=8,
∴PB=PQ=8 ![]() ,
,
∴PB旋转到PQ所扫过的面积= ![]() =32π.
=32π.
②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F.设PE=x.
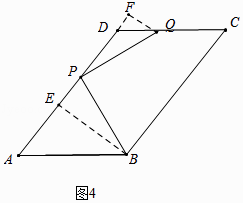
易证△PBE≌△QPF,
∴PE=QF=x,EB=PF=8,
∴DF=AE+PE+PF﹣AD=x﹣1,
∵CD∥AB,
∴∠FDQ=∠A,
∴tan∠FDQ=tanA= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x=4,
∴PE=4, ![]() =4
=4 ![]() ,
,
在Rt△PEB中,PB=, ![]() =4
=4 ![]() ,
,
∴PB旋转到PQ所扫过的面积= ![]() =20π
=20π
③如图5中,
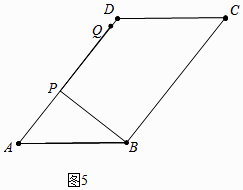
当点Q落在AD上时,易知PB=PQ=8,
∴PB旋转到PQ所扫过的面积= ![]() =16π,
=16π,
综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π
【解析】(1)分两种情形①当点Q在平行四边形ABCD内时,②当点Q在平行四边形ABCD外时,分别求解即可;(2)如图2中,连接BQ,作PE⊥AB于E.在Rt△APE中,tanA= ![]() =
= ![]() ,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP=
,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP= ![]() =2,推出EB=2k,推出AB=5k=10,可得k=2,由此即可解决问题;(3)分三种情形分别求解即可;
=2,推出EB=2k,推出AB=5k=10,可得k=2,由此即可解决问题;(3)分三种情形分别求解即可;
【考点精析】通过灵活运用平行四边形的性质和解直角三角形,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.

 名校课堂系列答案
名校课堂系列答案