题目内容
【题目】如图，Rt△ABC中，∠BAC=90°，将△ABC绕点C逆时针旋转，旋转后的图形是△A′B′C，点A的对应点A′落在中线AD上，且点A′是△ABC的重心，A′B′与BC相交于点E，那么BE：CE= ．
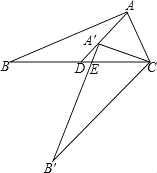
【答案】4：3
【解析】
试题分析：∵∠BAC=90°，A′是△ABC重心，
∴BD=DC=AD，DA′=
AA′=
AD=
BC，
∵△A′CB′S是由△ABC旋转得到，
∴CA′=CA，BC=CB′，∠ACB=∠A′CB′=∠DAC，∠CA′B′=90°，
∴∠CAA′=∠CA′A=∠DAC，∠DA′B′+′CA′A=90°，∠B′+∠A′CB′=90°，
∴∠DA′B′=∠B′
∴DA′∥CB′，
∴
=
=
，设DE=k，则EC=6k，BE=DC=7k，BE=8k，
∴BE：CE=8k：6k=4：3．
故答案为4：3．
练习册系列答案
相关题目
【题目】弹簧挂上物体后会伸长，测得某一弹簧的长度y(cm)与悬挂物体的质量x(kg)有下面一组对应值．
根据上述对应值回答：
(1)弹簧不挂物体时的长度是多少？
(2)当所挂物体的质量x每增加1 kg，弹簧长度如何变化？
(3)求弹簧总长y( cm)与所挂物体质量x( kg)的函数关系式，并指出是什么函数？
(4)当所挂物体的质量为10 kg时，弹簧的长度是多少？
x( kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y( cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
