题目内容
 如图已知△ABC中,AB=AC,∠ABD=60°,且∠ADB=90°-
如图已知△ABC中,AB=AC,∠ABD=60°,且∠ADB=90°-| 1 | 2 |
分析:延长BD至E,使DE=DC,连接CE,AE,得出∠DCE=∠DEC=
∠BDC,由∠ADE=360°-∠ADB-∠BDC-∠CDE,证出∠ADE=∠ADC,推出△ADC≌△ADE,得到AC=AE=AB,根据等边三角形的判定和性质推出AB=BE,即可推出答案.
| 1 |
| 2 |
解答: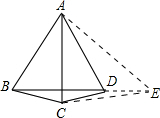 证明:延长BD至E,使DE=DC,连接CE,AE,
证明:延长BD至E,使DE=DC,连接CE,AE,
∴∠DCE=∠DEC=
∠BDC,
∴∠ADE=360°-∠ADB-∠BDC-∠CDE=360°-(90°-
∠BDC)-∠BDC-(180°-∠BDC)
=90°+
∠BDC,
∵∠ADC=∠ADB+∠BDC=90°-
∠BDC+∠BDC,
∴∠ADE=∠ADC,
∵AD=AD,
∴△ADC≌△ADE,
∴AC=AE=AB,
由于∠ABD=60°,
∴△ABE为等边三角形,
∴AB=BE=BD+DE=BD+CD,
即:AB=BD+DC.
 证明:延长BD至E,使DE=DC,连接CE,AE,
证明:延长BD至E,使DE=DC,连接CE,AE,∴∠DCE=∠DEC=
| 1 |
| 2 |
∴∠ADE=360°-∠ADB-∠BDC-∠CDE=360°-(90°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
∵∠ADC=∠ADB+∠BDC=90°-
| 1 |
| 2 |
∴∠ADE=∠ADC,
∵AD=AD,
∴△ADC≌△ADE,
∴AC=AE=AB,
由于∠ABD=60°,
∴△ABE为等边三角形,
∴AB=BE=BD+DE=BD+CD,
即:AB=BD+DC.
点评:本题主要考查对等边三角形的性质和判定,等腰三角形的性质和判定,全等三角形的性质和判定,四边形的内角和定理等知识点的理解和掌握,正确作辅助线并利用性质进行推理是解此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图已知△ABC中,∠B和∠C外角平分线相交于点P.
如图已知△ABC中,∠B和∠C外角平分线相交于点P. (2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域.
(2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域. 如图已知△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,DE垂直平分BC,AB=4cm,那么△CDE的周长是
如图已知△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,DE垂直平分BC,AB=4cm,那么△CDE的周长是 如图已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=6厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度与点P的运动速度相等,经过
如图已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=6厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度与点P的运动速度相等,经过