题目内容
 (2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域.
(2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域.分析:首先过点作AM⊥BC于点M,由AB=AC=10,BC=16,根据等腰三角形的性质与勾股定理,即可求得AM的长,又由四边形DEFG是矩形,易证得△ADG∽△ABC,由相似三角形对应高的比等于相似比,即可得方程
=
,则可表示出DG的长,继而求得答案.
| DG |
| 16 |
| 6-x |
| 6 |
解答: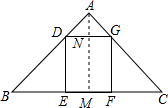 解:过点作AM⊥BC于点M,
解:过点作AM⊥BC于点M,
∵AB=AC=10,BC=16,
∴BM=
BC=8,
在Rt△ABM中,AM=
=6,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴
=
,
解得:DG=-
x+16,
∴y=S矩形DEFG=DE•DG=x•(-
x+16)=-
x2+16x(0<x<6).
 解:过点作AM⊥BC于点M,
解:过点作AM⊥BC于点M,∵AB=AC=10,BC=16,
∴BM=
| 1 |
| 2 |
在Rt△ABM中,AM=
| AB2-BM2 |
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴
| DG |
| 16 |
| 6-x |
| 6 |
解得:DG=-
| 8 |
| 3 |
∴y=S矩形DEFG=DE•DG=x•(-
| 8 |
| 3 |
| 8 |
| 3 |
点评:此题考查了相似三角形的判定与性质、矩形的性质以及勾股定理.此题难度适中,注意辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
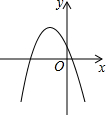 (2013•嘉定区一模)已知抛物线y=-x2+bx+c如图所示,那么b、c的取值范围是( )
(2013•嘉定区一模)已知抛物线y=-x2+bx+c如图所示,那么b、c的取值范围是( )