题目内容
 22、证明:角的平分线上的点到角的两边的距离相等.
22、证明:角的平分线上的点到角的两边的距离相等.已知:如图:∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证:
PD
=PE
证明:∵PD⊥OA,PE⊥OB
∴∠
PDO
=∠PEO
=90°在△PDO和△PEO中,
∴△PDO≌△PEO(
AAS
)∴PD=PE (
全等三角形的对应边相等
)分析:首先点到直线的距离是垂线段的长,即PD=PE;证明△PDO≌△PEO的三个条件是:∠AOC=∠BOC,∠PDO=∠PEO=90°,OP是公共边,符合AAS.据此作答.
解答:已知:如图:∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,
∴△PDO≌△PEO( AAS),
∴PD=PE ( 全等三角形的对应边相等).
求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,
∴△PDO≌△PEO( AAS),
∴PD=PE ( 全等三角形的对应边相等).
点评:此题考查角平分线的性质定理的证明,应用了全等三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.
23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D. 七(1)班同学上数学活动课,他们对一个角的平分线作如下研究(如图).他们先用角尺做了平分这个角的方案设计:
七(1)班同学上数学活动课,他们对一个角的平分线作如下研究(如图).他们先用角尺做了平分这个角的方案设计: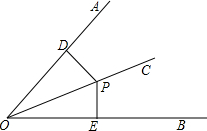 证明:角的平分线上的点到角的两边的距离相等.
证明:角的平分线上的点到角的两边的距离相等.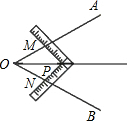 七(1)班同学上数学活动课,他们对一个角的平分线作如下研究(如图).他们先用角尺做了平分这个角的方案设计:
七(1)班同学上数学活动课,他们对一个角的平分线作如下研究(如图).他们先用角尺做了平分这个角的方案设计: