题目内容
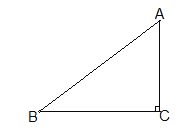
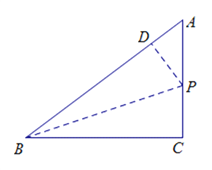
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)用含t的式子表示出AP,CP的长,用勾股定理列方程求解;
(2)利用角平分线的性质定理,用含t的式子表示出AP,PD的长,用勾股定理列方程求解;
(3)AC不动,点P是动点,所以需要分类讨论,分别以A,C,P为等腰三角形的顶点构成的等腰三角形,然后用勾股定理列方程求解.
试题解析:
Rt△ABC中,由勾股定理得AC=3.
(1)根据题意得AB+BP=2t,所以BP=2t-AB=2t-5,
则AP=2t-5,PC=BC-PB=4-(2t-5)=9-2t.
Rt△APC中,由勾股定理得:AC2+PC2=AP2,即32+(9-2t)2=(2t-5)2,解得t=![]() .
.
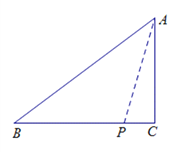
(2)过点P作PD⊥AB于点D.
因为BP平分∠ABC,∠C=90°,所以PD=PC,BD=BC.
根据题意得,AB+BC+CP=2t,所以CP=2t-9,
则DP=2t-9,AP=3-(2t-9)=12-2t.
Rt△APD中,AD=AB-BD=5-4=1,由勾股定理得:
PD2+AD2=AP2,即12+(2t-9)2=(12-2t)2,解得t=![]() .
.
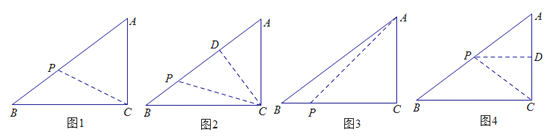
(3) 如图1,当AP=AC时,AP=3,2t=3,t=![]() .
.
如图2,当CA=CP,点P在AB上时,过点C作CD⊥AB于点D,则AD=PD.
因为CD×AB=AC×BC,所以5CD=3×4,CD=![]() .
.
Rt△ACD中,由勾股定理得AD=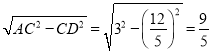 .
.
因为AP=2AD,所以t=2AD÷2=AD=![]() .
.
如图3,当CA=CP,点P在BC上时,CP=CA=3.
则BP=BC-BP=4-3=1,AB+BP=5+1=6.
所以t=6÷2=3.
如图4,当PA=PC时,过点P作PD∥BC交AC于点D,则PD垂直平分AC,所以AP=BP=![]() ,t=
,t=![]() ÷2=
÷2=![]() .
.
综上所述,当t=![]() ,
, ![]() ,3,
,3, ![]() 时,△ACP为等腰三角形.
时,△ACP为等腰三角形.

 小学课时特训系列答案
小学课时特训系列答案【题目】列方程组解古算题:今有共买物,人出八,赢三;人出七,不足四,问人数、物价几何?
题目大意是:几个人共同买一件物品,每人出8钱,余3钱;每人出7钱,缺4钱,求参与共同购物的有几人?物品价值多少钱?
【题目】某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如下:
锻炼时间/h | 5 | 6 | 7 | 8 |
人数 | 6 | 15 | 10 | 4 |
则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
A.6h,6hB.6h,15hC.6.5h,6hD.6.5h,15h