题目内容
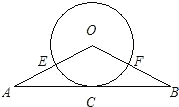 如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
(1)求证:AB是⊙O的切线;
(2)若△ABO腰上的高等于底边的一半,且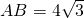 ,求
,求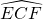 的长.
的长.
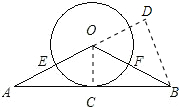 (1)证明:连接OC.
(1)证明:连接OC.∵OA=OB,AC=BC,
∴OC⊥AB.
∵C在⊙O上,
∴AB是⊙O的切线.
(2)解:过B点作BD⊥AO,交AO的延长线于D点.
由题意有AB=2BD,
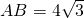 .
.在Rt△ABD中,根据正弦定义
 ,
,∴∠A=30度.
在Rt△ACO中,
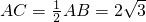 ,∠A=30°,
,∠A=30°,则AO=2OC.
由勾股定理,求得OC=2.
∵OA=OB,且∠A=30°,
∴∠AOB=120度.
由弧长公式可求得
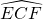 的长为
的长为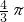 .
.分析:由OA=OB,AC=BC,即可推出OC⊥AB,即AB是⊙O的切线;
根据三角函数公式及勾股定理求得∠A=30°,OC=2,又因为OA=OB,从而得出∠AOB=120度.由弧长公式可求得
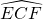 的长为
的长为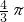 .
.点评:此题考查学生对切线的判定,弧长公式,及解直角三角形的综合运用能力.

练习册系列答案
相关题目
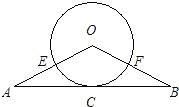 如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.

 如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.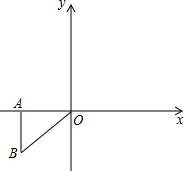 如图,△ABO中,O是坐标原点,A
如图,△ABO中,O是坐标原点,A (2013•牡丹江)如图,△ABO中,AB⊥OB,OB=
(2013•牡丹江)如图,△ABO中,AB⊥OB,OB=