题目内容
 如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB中点C,且分别交OA、OB于点E、F.(1)求证:AB是⊙O切线;
(2)若∠B=30°,且AB=4
| 3 |
 |
| ECF |
分析:(1)连接OC,利用等边三角形底边上的中线即是底边上的高,即可证明.
(2)由∠B=30°,可求出圆心角,AB=4
,解直角三角形可求出圆的半径,然后利用弧长公式计算.
(2)由∠B=30°,可求出圆心角,AB=4
| 3 |
解答: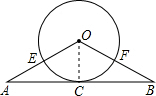 证明:(1)连接OC,∵OA=OB,C是AB的中点,
证明:(1)连接OC,∵OA=OB,C是AB的中点,
∴OC⊥AB.
∵点C在⊙O上,
∴AB是⊙O切线.(4分)
(2)∵OA=OB,∠B=30°,
∴∠EOF=120°.
∵C为AB的中点,AB=4
,
∴BC=2
.
在Rt△OCB中,令OC=r,则OB=2r,
列出方程为(2r)2-r2=(2
)2
解得:r=2.(3分)
的长=
=
π.(3分)
 证明:(1)连接OC,∵OA=OB,C是AB的中点,
证明:(1)连接OC,∵OA=OB,C是AB的中点,∴OC⊥AB.
∵点C在⊙O上,
∴AB是⊙O切线.(4分)
(2)∵OA=OB,∠B=30°,
∴∠EOF=120°.
∵C为AB的中点,AB=4
| 3 |
∴BC=2
| 3 |
在Rt△OCB中,令OC=r,则OB=2r,
列出方程为(2r)2-r2=(2
| 3 |
解得:r=2.(3分)
 |
| ECF |
| 120×π×2 |
| 180 |
| 4 |
| 3 |
点评:本题综合考查了等边三角形的三线合一性质,及弧长公式的计算能力.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
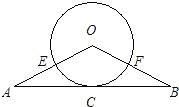 如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
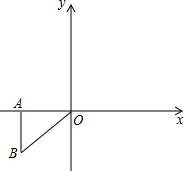 如图,△ABO中,O是坐标原点,A
如图,△ABO中,O是坐标原点,A (2013•牡丹江)如图,△ABO中,AB⊥OB,OB=
(2013•牡丹江)如图,△ABO中,AB⊥OB,OB=