Question

【题目】如图，抛物线y=ax2+bx+c（a≠0）的图象经过点A，B，C，已知点A的坐标为（﹣3，0），点B的坐标为（1，0），点C在y轴的正半轴上，且∠CAB=30°，若直线l：y=x+m从点C开始沿y轴向下平移．

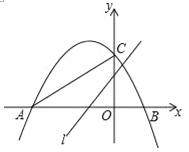
（1）当直线l上点D满足DA=DC且∠ADC=90°时，m的值为 _________ ；

（2）以动直线l为对称轴，线段AC关于直线l的对称线段A′C′与抛物线有交点，写出m的取值范围 _________．

Answer 1

【答案】（1）2﹣3；（2）﹣＜m＜．

【解析】

试题分析：如图1所示：过点D作DE⊥y轴，垂足为E，过点A作AF⊥DE，垂足为F．

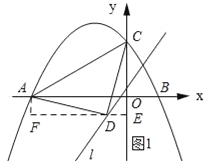
∵∠ADC=90°，

∴∠ADF+∠CDE=90°．

∵∠ADF+∠DAF=90°，

∴∠DAF=∠CDE．

∵在Rt△AFD和Rt△DEC中，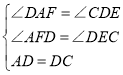

∴Rt△AFD≌Rt△DEC．

∴AF=DE，DF=CE．

设点D的坐标为（x， x+m），则x=x+m=①，x+3=﹣x﹣m②．

①+②得：2x+3=，

解得：x=．

∴=×+m．

解得：m=2﹣3．

（2）∵OA=3，∠CAB=30°，

∴OC=．

∴C（0，）．

①当直线l经过点C时．

∵将C（0，）代入y=x+m得：

∴m=．

②如图2所示：

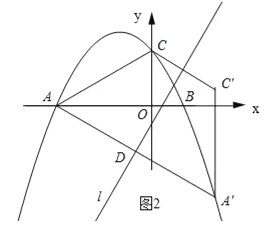
设抛物线的解析式为y=a（x+3）（x﹣1）．

∵将C（0，）代入得：﹣3a=，解得：a=﹣，

∴抛物线的解析式为y=﹣x2﹣x+．

∵点A与点A′关于l对称，

∴AA′⊥l．

∴直线AA′的一次项系数为﹣．

设直线AA′的解析式为y=﹣x+b．

∵将A（﹣3，0）代入得：+b=0，解得：b=﹣

∴直线AA′的解析式为y=﹣x﹣．

将y=﹣x﹣代入y=﹣x2﹣x+得：﹣ x﹣=﹣x2﹣x+．

整理得：x2+x﹣6=0．

解得：x1=2，x2=﹣3．

∵将x=2代入y=﹣x﹣得：y=﹣，

∴点A′的坐标为（2，﹣）．

∴D（﹣，﹣）．

将D（﹣，﹣）代入y=+m得：﹣ +m=﹣，解得：m=﹣．

∴m的取值范围是﹣＜m＜．

故答案为：（1）2﹣3；（2）﹣＜m＜．