题目内容
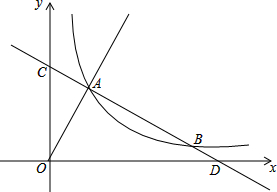 已知直线y=-
已知直线y=-| 1 |
| 2 |
| 5 |
| 2 |
| m |
| x |
(1)求OA的长度;
(2)求m的值;
(3)若B点横坐标为整数,请直接写出点B的坐标,并在射线OA上找一点P,使以A、B、P为顶点的三角形与△COD相似.
考点:反比例函数综合题
专题:代数几何综合题,数形结合
分析:(1)首先求得OC和OD的长度,然后根据△OCD的面积公式即可求得OA的长;
(2)根据一次函数与直线OA垂直,即可求得直线OA的解析式,然后解OA的解析式和直线AB的解析式组成的方程组即可求得A的坐标,利用待定系数法即可求得m的值;
(3)分△BAP∽△COD和△PAB∽△COD两种情况进行讨论,求得AP的长度,然后利用相似三角形的性质求得P的坐标.
(2)根据一次函数与直线OA垂直,即可求得直线OA的解析式,然后解OA的解析式和直线AB的解析式组成的方程组即可求得A的坐标,利用待定系数法即可求得m的值;
(3)分△BAP∽△COD和△PAB∽△COD两种情况进行讨论,求得AP的长度,然后利用相似三角形的性质求得P的坐标.
解答:解:(1)在y=-
x+
中,令x=0,解得:y=
;
令y=0,解得:x=5,
则C的坐标是(0,
),D的坐标是(5,0).
则OC=
,OD=5.
则CD=
=
,
∵S△OCD=
OC•OD=
CD•OA,
∴OA=
=
=
;
(2)∵OA⊥AB,
∴直线OA的解析式是y=2x.
根据题意得:
,
解得:
,
则A的坐标是(1,2),代入y=
,得:m=2;
(3)根据题意得:
,
解得:
或
,
则B的坐标是(4,
).
则AB=
=
,
当△BAP∽△COD时,
=
,即
=
,解得:AP=3
,则OP=4
,
过P作PF⊥x轴于F,过A作AE⊥x轴于E.
则△OAE∽△POF,
∴
=
=
=
=4,
∴OF=4OE=4,PF=4AE=8,
则P的坐标是(4,8);
当△PAB∽△COD时,
=
,即
=
,解得:PA=
,
同理可得P的坐标是:(
,7).
则P的坐标是:(4,8)或(
,7).
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
令y=0,解得:x=5,
则C的坐标是(0,
| 5 |
| 2 |
则OC=
| 5 |
| 2 |
则CD=
(
|
5
| ||
| 2 |
∵S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=
| OC•OD |
| CD |
| ||||
|
| 5 |
(2)∵OA⊥AB,
∴直线OA的解析式是y=2x.
根据题意得:
|
解得:
|
则A的坐标是(1,2),代入y=
| m |
| x |
(3)根据题意得:
|

解得:
|
|
则B的坐标是(4,
| 1 |
| 2 |
则AB=
(4-1)2+(2-
|
3
| ||
| 2 |
当△BAP∽△COD时,
| AP |
| OD |
| AB |
| OC |
| AP |
| 5 |
| ||||
|
| 5 |
| 5 |
过P作PF⊥x轴于F,过A作AE⊥x轴于E.
则△OAE∽△POF,
∴
| OF |
| OE |
| PF |
| AE |
| OP |
| OA |
4
| ||
|
∴OF=4OE=4,PF=4AE=8,
则P的坐标是(4,8);
当△PAB∽△COD时,
| PA |
| OC |
| AB |
| OD |
| PA | ||
|
| ||||
| 5 |
3
| ||
| 4 |
同理可得P的坐标是:(
| 7 |
| 2 |
则P的坐标是:(4,8)或(
| 7 |
| 2 |
点评:本题考查了待定系数法求函数的解析式,以及相似三角形的判定与性质,通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,正确进行讨论是关键.

练习册系列答案
相关题目
平面内四条直线最少有a个交点,最多有b个交点,则a+b=( )
| A、6 | B、4 | C、2 | D、0 |

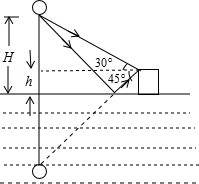 如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H.
如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H. 如图所示,已知⊙O1与⊙O2外切于点E.求证:若⊙O1的直径AB与⊙O2的直径CD平行,则直线AD和BC相交于点E.
如图所示,已知⊙O1与⊙O2外切于点E.求证:若⊙O1的直径AB与⊙O2的直径CD平行,则直线AD和BC相交于点E.