题目内容
【题目】有一个运算程序,可以使:![]() (n为常数)时,
(n为常数)时,![]() ,
,![]() .现在已知
.现在已知![]() ,那么
,那么![]() .
.
【答案】-6043.
【解析】利用归纳法解答,根据题目给出的例子,求得2⊕1=2+1=3,2⊕2=3-2=1,3⊕2=1+1=2,3⊕3=2-2=0,同样的我们可以求得4⊕4=-1,5⊕5=-2…,2016⊕2016=-2013.规律为:前项增一,结果加一,后项增一,结果减二,….
解:规律为前一项增一,结果加一,后一项增一,结果减二,…,则
1⊕1=2,(其中x=1,y=1,n=2)
∴2⊕1=3,
1⊕2=0,(此时x=1,y=2,n=-1)
2⊕2=-1=2-3×1,
3⊕3=-4=2-3×2,
4⊕4=-7=2-3×3,
5⊕5=-10=2-3×4,
…
∴2016⊕2016=-10=2-3×(2016-1)=-6043.
故答案为:-6043.
“点睛”解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.关键是分析得到⊕的运算规律.

 星级口算天天练系列答案
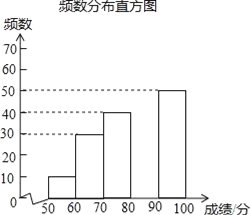
星级口算天天练系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?