题目内容
已知,如图,![]() 小于半圆周,它所在的圆的圆心为O,半径为13,弦AB的长为24;C是弦AB上的一个动点(异于A、B),过C作AB的垂线交
小于半圆周,它所在的圆的圆心为O,半径为13,弦AB的长为24;C是弦AB上的一个动点(异于A、B),过C作AB的垂线交![]() 于点P,以PC为直径的圆交AP于点D;E为AP的中点,连结OE.
于点P,以PC为直径的圆交AP于点D;E为AP的中点,连结OE.
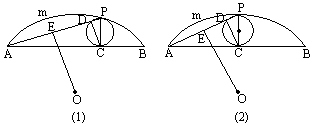
(1)当点D、E不重合时,如图(1),求证OE∥CD;
(2)当点C是弦AB的中点时,如图(2),求PD的长;
(3)当点D、E重合时,请你推断∠PAB的大小为多少度(只需给出结论,不必给出证明).
答案:
解析:
解析:
|
(1)因为CP是小圆的直径,所以CD⊥AP,又E是AP的中点.所以OE⊥AP,所以CD∥OE. (2)连结OA,∵C是弦AB的中点,CP⊥AB,所以P、C、O三点共线.在Rt△ACO中OA=13,AC= (3)∠PAB= |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,并且每两个小圆的公共部分的面积都小于
,并且每两个小圆的公共部分的面积都小于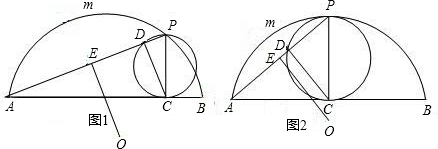


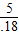 π?请说出你的结论,并给出证明.
π?请说出你的结论,并给出证明.