Question

已知：如图，弓形AmB小于半圆，它所在圆的圆心为O，半径为13，弦AB的长为24；C是弦AB上的一动点（异于A、B），过C作AB的垂线交弧AB于点P，以PC为直径的圆交AP于点D；E是AP的中点，连接OE．
（1）当点D、E不重合时（如图1），求证：OE∥CD；
（2）当点C是弦AB的中点时（如图2），求PD的长；
（3）当点D、E重合时，请你推断∠PAB的大小为多少度（只需写出结论，不必给出证明）

Answer 1

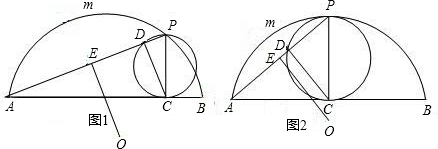
分析：（1）根据圆周角定理求出∠CDP=90°，根据垂径定理求出OE⊥AP，即可推出答案；
（2）根据垂径定理求出OC⊥AB，根据勾股定理求出OC、AP，由切割线定理求出AD，计算AP-AD即可；
（3）根据直角三角形的性质和等腰三角形的性质即可求出∠PAB．

解答：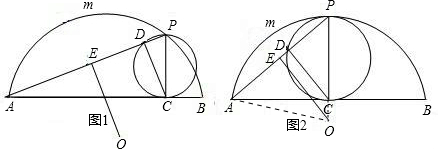
（1）证明：∵CP是直径，
∴∠CDP=90°，
∵OE过圆心O，AE=PE，
∴OE⊥AP，
∴OE∥CD．

（2）解：连接OC、AO，
∵AC=BC，
∴OC⊥AB，
∵PC⊥AB，
∴P、C、O三点共线，
由勾股定理得：OC=

OA2-AC2

=5，
∴PC=13-5=8，
由勾股定理得：AP=

AC2+PC2

=4

13

，
由切割线定理得：AC²=AD•AP，
∴AD=

36 13

13

，
PD=AP-AD=

16 13

13

，
答：PD的长是

16 13

13

．

（3）答：∠PAB=45°．

点评：本题主要考查对圆周角定理，勾股定理，垂径定理，直角三角形的性质，等腰三角形的性质等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．