Question

【题目】如图，已知一次函数y=﹣x+6的图象与坐标轴交于A、B两点，AE平分∠BAO，交x轴于点E．

（1）求点B的坐标及直线AE的表达式；

（2）过点B作BF⊥AE，垂足为F，在y轴上有一点P，使线段PE+PF的值最小，求点P的坐标；

（3）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F，以EF为边作正方形EFMN，当点M落在坐标轴上时，求E点坐标．

Answer 1

【答案】（1）B（8，0），y=﹣2x+6；（2）P（0，﹣）；（3）点E坐标为（，0）或（6，0）．

【解析】

（1）设OE=x，作EM⊥AB于M．在Rt△EBM中，根据EM2+BM2=EB2，可得x2+42=（8-x）2，求出x即可解决问题；

（2）如图2中，作点E关于y轴的对称点E′，连接FE′交y轴于P，此时PE+PF的值最小．想办法切线直线FE′的解析式即可解决问题；

（3）①如图3中，当点M在y轴上时，作FP⊥OB于P，FQ⊥OM于Q．利用全等三角形的性质，证明四边形OPFQ是正方形即可解决问题；②如图4中，当点M在x轴上时，易知OA=OE=6，可得E（6，0）.

（1）如图1中，

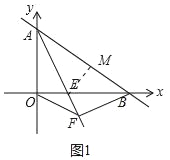
∵一次函数y=﹣x+6的图象与坐标轴交于A、B点，

∴A（0，6），B（8，0），设OE=x，作EM⊥AB于M．

∵AE平分∠OAB，OE⊥OA，

∴OE=EM=x，

在△AEO和△AEM中，，

∴△AEO≌△AEM，

∴AM=AO=6，

∵OA=6，OB=8，∠AOB=90°，

∴AB===10，

∴BM=4，

在Rt△EBM中，∵EM2+BM2=EB2，

∴x2+42=（8﹣x）2，

∴x=3，

∴E（3，0），

设直线AE的解析式为y=kx+b，

则，

解得，

∴直线AE的解析式为y=﹣2x+6；

（2）如图2中，作点E关于y轴的对称点E′，连接FE′交y轴于P，此时PE+PF的值最小．

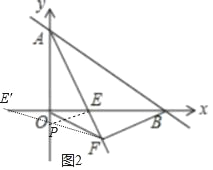
∵BF⊥AE，

∴直线BF的解析式为y=x﹣4，

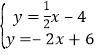由 解得，

∴F（4，﹣2），

∴直线FE′的解析式为y=﹣x﹣，

∴P（0，﹣）．

（3）①如图3中，当点M在y轴上时，作FP⊥OB于P，FQ⊥OM于Q．

∵四边形EFMN是正方形，

∴FE=FM，∠EFM=∠PFQ，

∴∠EFP=∠MFQ，

∵∠FPE=∠FQM=90°，

∴△FPE≌△FQM，

∴FP=FQ，四边形OPFQ是正方形，设边长为x．

∵∠AEO=∠BEF，∠AOE=∠PFE=90°，

∴∠FAQ=∠FBP，

∵∠AQF=∠BPF=90°，

∴△AQF≌△BPF，

∴AQ=BP，

∴6+x=8﹣x

∴x=1，

∴F（1，﹣1），

∴直线AF的解析式为y=﹣7x+6，

∴E（，0）；

②如图4中，当点M在x轴上时，易知OA=OE=6，可得E（6，0）．

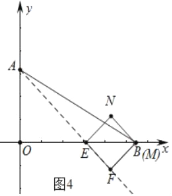
综上所述，满足条件的点E坐标为（，0）或（6，0）．