题目内容
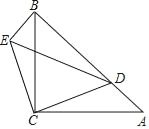
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=3![]() ,点D在AB上,且BD=2AD,连接CD,将线段CD绕点C逆时针方向旋转90°至CE,连接BE,DE.
,点D在AB上,且BD=2AD,连接CD,将线段CD绕点C逆时针方向旋转90°至CE,连接BE,DE.
(1)求证:△ACD≌△BCE;
(2)求线段DE的长度.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)先根据旋转的性质,由线段CD绕点C逆时针旋转90°,于是可得∠ACD=∠BCE,然后根据SAS即可得到△ACD≌△BCE;(2)先在RT△中利用勾股定理求出AB=6,由BD=2AD得到AD=2,BD=4,再证明∠DBE=90°,BE=2,然后在RT△BDE中利用勾股定理即可求出DE的长度.
详解:(1)证明:∵将线段CD绕点C逆时针方向旋转90°至CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
即∠ACD=∠BCE.
在△ACD与△BCE中,
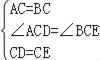 ,
,
∴△ACD≌△BCE;
(2)解:∵在Rt△ABC中,∠C=90°,AC=BC=3![]() ,
,
∴AB=6.
∵BD=2AD,
∴AD=2,BD=4.
由(1)可知△ACD≌△BCE,
∴∠CBE=∠A=45°,BE=AD=2,
∴∠DBE=∠ABC+∠CBE=90°.
∵在Rt△BDE中,∠DBE=90°,
∴DE2=BE2+BD2,
∴DE=![]() =2
=2![]() .
.
点睛:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质,勾股定理等知识.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目