题目内容
如图,给出下列论断:
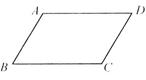
(1)AB∥DC;
(2)AD∥BC;
(3)∠A+∠B=180°;
(4)∠B+∠C=180°,以其中一个作为题设,一个作为结论,写出一个真命题.想一想,若连接BD,你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.

(1)AB∥DC;
(2)AD∥BC;
(3)∠A+∠B=180°;
(4)∠B+∠C=180°,以其中一个作为题设,一个作为结论,写出一个真命题.想一想,若连接BD,你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.
见解析
本题考查的是平行线的判定与性质
根据平行线的性质:两直线平行,同旁内角互补,得到:若(1)AB∥DC则有(4)∠B+∠C=180;由(2)AD∥BC可以得到(3)∠A+∠B=180°.反之,根据平行线的判定,也成立.连接BD,则BD截AD和BC,因而可以得到:若AD∥BC,则可以得到∠ADB=∠DBC.
以一个作题设,一个作结论,写出一个真命题是:若AB∥DC则有∠B+∠C=180;
若连接BD,写出一个真命题是:若AD∥BC,则可以得到∠ADB=∠DBC.
证明:∵AD∥BC,∴∠ADB=∠DBC(两直线平行,内错角相等).
根据平行线的性质:两直线平行,同旁内角互补,得到:若(1)AB∥DC则有(4)∠B+∠C=180;由(2)AD∥BC可以得到(3)∠A+∠B=180°.反之,根据平行线的判定,也成立.连接BD,则BD截AD和BC,因而可以得到:若AD∥BC,则可以得到∠ADB=∠DBC.
以一个作题设,一个作结论,写出一个真命题是:若AB∥DC则有∠B+∠C=180;
若连接BD,写出一个真命题是:若AD∥BC,则可以得到∠ADB=∠DBC.
证明:∵AD∥BC,∴∠ADB=∠DBC(两直线平行,内错角相等).

练习册系列答案
相关题目
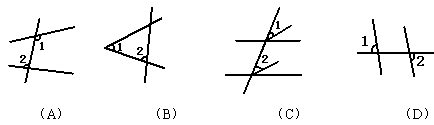
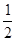 ∠A
∠A 且
且 求
求 的度数.
的度数.
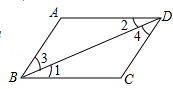
 平分
平分 ,
, ,
, 相等吗?请说明理由.
相等吗?请说明理由.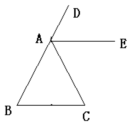
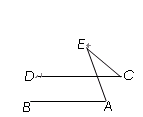
 DE为半径作弧,在∠AOB内两弧交于点G
DE为半径作弧,在∠AOB内两弧交于点G