Question

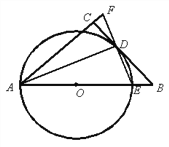
【题目】如图1，在△ABC中，∠BAC=90°，AB=AC=4，D是BC上一个动点，连接AD，以AD为边向右侧作等腰直角△ADE，其中∠ADE=90°．

（1）如图2，G，H分别是边AB，BC的中点，连接DG，AH，EH．求证：△AGD∽△AHE；

（2）如图3，连接BE，直接写出当BD为何值时，△ABE是等腰三角形；

（3）在点D从点B向点C运动过程中，求△ABE周长的最小值．

Answer 1

【答案】（1）证明见解析；（2）当BD=0或或时，△ABE是等腰三角形.；（3）△ABE周长最小值为．

【解析】（1）根据等腰直角三角形的性质和相似三角形的判定解答即可；

（2）分三种情况：

①当B与D重合时，即BD=0，如图3，此时AB=BE；

③当AB=AE时，如图4，此时E与C重合，可得BD的长；

③当AB=BE时，如图5，作辅助线，构建等腰直角三角形和全等三角形，证明△ADM≌△DEG，和△EMG是等腰直角三角形，则ME=MG，根据（1）得：△AHD∽△AME，且，可计算BD的长；

（3）先确定△ABE周长的最小值时，E的位置：作点B关于直线MC的对称点N，连接AN交MC于点E′，此时△ABE′就是所求周长最小的△ABE；证明四边形ABMC是正方形，根据△ABD∽△AME，得∠AME=∠ABD=45°，知点E在射线MC上，利用勾股定理求AN的长，根据周长定义可得结论．

（1）证明：如图2，由题意知△ABC和△ADE都是等腰直角三角形，

∴∠B=∠DAE=45°．

∵H为BC中点，

∴AH⊥BC．

∴∠BAH=45°=∠DAE．

∴∠GAD=∠HAE．

在等腰直角△BAH和等腰直角△DAE中，

AH＝AB＝AG，AE＝AD．

∴，

∴△AGD∽△AHE；

（2）解：分三种情况：

①当B与D重合时，即BD=0，如图3，此时AB=BE；

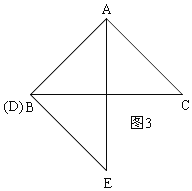
③当AB=AE时，如图4，此时E与C重合，

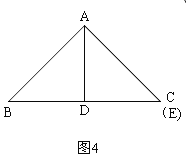
∴D是BC的中点，

∴BD=BC=2；

③当AB=BE时，如图5，过E作EH⊥AB于H，交BC于M，连接AM，过E作EG⊥BC于G，连接DH，

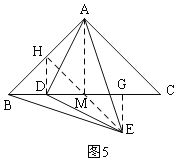
∵AE=BE，EH⊥AB，

∴AH=BH，

∴AM=BM，

∵∠ABC=45°，

∴AM⊥BC，△BMH是等腰直角三角形，

∵AD=DE，∠ADE=90°，

易得△ADM≌△DEG，

∴DM=EG，

∵∠EMG=∠BMH=45°，

∴△EMG是等腰直角三角形，

∴ME=MG，

由（1）得：△AHD∽△AME，且，

∴∠AHD=∠AME=135°，ME=DH，

∴∠BHD=45°，MG=DH，

∴△BDH是等腰直角三角形，

∴BD=DH=EG=DM=；

综上所述，当BD=0或或2时，△ABE是等腰三角形；

（3）解：当点D与点B重合时，点E的位置记为点M，连接CM，如图6，

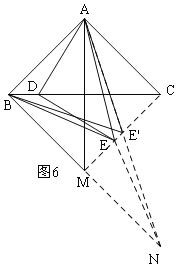
此时，∠ABM=∠BAC=90°，∠AMB=∠BAM=45°，BM=AB=AC．

∴四边形ABMC是正方形．

∴∠BMC=90°，

∴∠AMC=∠BMC-∠AMB=45°，

∵∠BAM=∠DAE=45°，

∴∠BAD=∠MAE，

在等腰直角△BAM和等腰直角△DAE中，

AM＝AB，AE＝AD．

∴．

∴△ABD∽△AME．

∴∠AME=∠ABD=45°

∴点E在射线MC上，

作点B关于直线MC的对称点N，连接AN交MC于点E′，

∵BE+AE=NE+AE≥AN=NE′+AE′=BE′+AE′，

∴△ABE′就是所求周长最小的△ABE．

在Rt△ABN中，

∵AB=4，BN=2BM=2AB=8，

∴AN＝．

∴△ABE周长最小值为AB+AN＝4+4．