Question

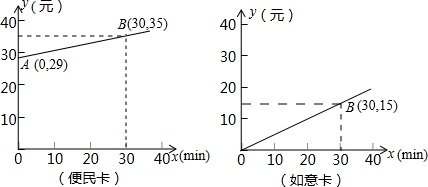
为发展电信事业，方便用户，电信公司对移动电话采取不同的收费方式，其中，所使用的“便民卡”与“如意卡”在某市范围内每月（30天）的通话时间x（min）与通话费y（元）的关系如图所示：
（1）分别求出通话费y₁，y₂与通话时间x之间的函数关系式；
（2）请帮用户计算，在一个月内使用哪一种卡便宜．

Answer 1

分析：（1）y₁与通话时间x成一次函数，y₂与x成正比例函数，使用待定系数法求解即可；
（2）当两种卡的收费相等时，可计算出通过时间x的值，当通话时间小于此值，则“如意卡”便宜；当通话时间大于此值，则，“便民卡”便宜．

解答：解：（1）设y₁=kx+b，将（0，29），（30，35）代入，
解得k=

1

5

，b=29，∴y1=

1

5

x+29，
又24×60×30=43200（min）
∴y1=

1

5

x+29（0≤x≤43200），
同样求得y2=

1

2

x(0≤x≤43200)；（3分）

（2）当y₁=y₂时，

1

5

x+29=

1

2

x，x=96

2

3

；（5分）
当y₁＜y₂时，

1

5

x+29＜

1

2

x，x＞96

2

3

．（6分）
所以，当通话时间等于96

2

3

min时，两种卡的收费相等，
当通话时间小于96

2

3

mim时，“如意卡便宜”，
当通话时间大于96

2

3

min时，“便民卡”便宜．（8分）

点评：本题意在考查学生利用待定系数法求解一次函数关系式，比较简单．