��Ŀ����
����Ŀ����һ����ֱ�Ĺ�·��ͬ������������A��C��B������ׯ��ij��ס��������ֱ��A��B���س�������������·������ʻ��C��ֹͣ���Ӽ׳��������׳�����C�صĹ��̣��ס�������������C�صľ���y��km����׳���ʻʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ���� 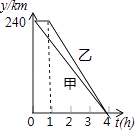
��1�����ٶ��� �� �ҵ��ٶ�����
��2���ֱ�����ס�������������C�صľ���y��km����׳���ʻʱ��t��h��֮��ĺ�����ϵʽ����д��ȡֵ��Χ��
��3�����ס���������C�غ�����ظù�·ԭ�ٶ���ʻ����׳���������Сʱ���������350km��
���𰸡�
��1��60km/h��80km/h
��2���⣺��������ã�y��=��60t+240��0��t��4����
��0��t��1ʱ��y��=240��
��1��t��4ʱ��y��=240��80��t��1��=��80t+320��
��y��= ![]() ��
��
��3���⣺���ס�����������C�ؼ�����ʻʱ��350�£�80+60��= ![]() ��h����
��h����
��80�� ![]() =200��km����200��240��
=200��km����200��240��
�൱�ס��������뿪C�ز����350kmʱ���ҳ���δ����A�أ�
�� ![]() +4=
+4= ![]() ��h����
��h����
�𣺼׳����� ![]() hʱ���������350km
hʱ���������350km
���������⣺��1��240��4=60��km/h���� 240�£�4��1��=80��km/h����
���Դ��ǣ�60km/h��80km/h��









