题目内容
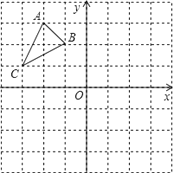
【题目】如图，在边长为1的正方形组成的网格中，△ABC的顶点均在格点上，点A、B、C的坐标分别是A（﹣2，3）、B（﹣1，2）、C（﹣3，1），△ABC绕点O顺时针旋转90°后得到△A1B1C1．
（1）在正方形网格中作出△A1B1C1；
（2）在旋转过程中，点A经过的路径弧A A1的长度为 ；（结果保留π）
（3）在y轴上找一点D，使DB+DB1的值最小，并求出D点坐标．
【答案】（1）作图见解析；（2）
π（3）D（0， 
）．
【解析】试题分析：（1）根据△ABC绕点O顺时针旋转90°后得到△A1B1C1，得出各对应点位置画出图象即可；
（2）利用弧长公式求出点A经过的路径
的长度即可；
（3）利用待定系数法求一次函数解析式进而得出D点坐标．
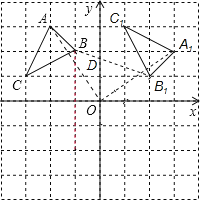
试题解析：（1）如图所示：
（2）在旋转过程中，点A经过的路径
的长度为： 
（3）∵B，B1在y轴两旁，连接BB1交y轴于点D，设D′为y轴上异于D的点，显然D′B+D′B1＞DB+DB1，
∴此时DB+DB1最小，
设直线BB1解析式为y=kx+b，依据题意得出：
，
解得：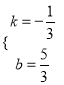 
，
∴y=-
x+
，
∴D（0， 
）．
【方法总结】此题主要考查了图形的旋转变换以及待定系数法求一次函数解析式等知识，根据数形结合得出D点位置是解题关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
