题目内容
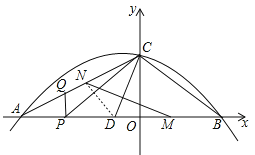
【题目】如图,抛物线y=ax2+bx+c为x轴的一交点为A(﹣6,0),与y轴的交点为C(0,3),且经过点G(﹣2,3).

(1)求抛物线的表达式.
(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值.
(3)若点B是抛物线与x轴的另一定点,点D、M在线段AB上,点N在线段AC上,∠DCB=∠CDB,CD是MN的垂直平分线,求点M的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)M(
;(3)M(![]() ,0).
,0).
【解析】试题分析:(1)把A、C、G三点坐标代入可求得抛物线解析式;
(2)先求直线AC的解析式,设P(x,0),可表示出OP、PQ,则可表示出S,再由二次函数的性质可求得S的最大值;
(3)由已知求得BD=BC=5,从而得到D点坐标,连接DN,可得出DN∥BC,从而DN为△ABC的中位线,得到DM的长,从而得到OM的长,进一步求得M点的坐标.
试题解析:(1)把A、C、G三点坐标代入抛物线解析式可得: 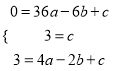 ,解得:
,解得: 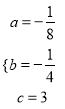 ,∴抛物线的表达式为
,∴抛物线的表达式为![]() ;
;
(2)∵C(0,3),∴可设直线AC解析式为![]() ,把A点坐标代入可得0=﹣6k+3,解得k=
,把A点坐标代入可得0=﹣6k+3,解得k=![]() ,∴直线AC解析式为
,∴直线AC解析式为![]() ,设P点坐标为(x,0)(x<0),则Q点坐标为(x,
,设P点坐标为(x,0)(x<0),则Q点坐标为(x, ![]() ),∴PQ=
),∴PQ=![]() ,PO=﹣x,∴S=
,PO=﹣x,∴S=![]() PQPO=
PQPO=![]() =
= ![]() =
=![]() ,∴△CPQ的面积S的最大值为
,∴△CPQ的面积S的最大值为![]() ;
;
(3)当y=0时, ![]() ,解得x=﹣6或x=4,∴B点坐标为(4,0),∴BC=
,解得x=﹣6或x=4,∴B点坐标为(4,0),∴BC=![]() =5,∵∠CDB=∠DCB,∴BD=BC=5,∴OD=BD﹣OB=5﹣4=1,∴D点坐标为(﹣1,0),∴D为AB中点,如图,连接DN,则DN=DM,∠NDC=∠MDC,∴∠NDC=∠
=5,∵∠CDB=∠DCB,∴BD=BC=5,∴OD=BD﹣OB=5﹣4=1,∴D点坐标为(﹣1,0),∴D为AB中点,如图,连接DN,则DN=DM,∠NDC=∠MDC,∴∠NDC=∠![]() BC=
BC=![]() ,∴OM=DM﹣OD=
,∴OM=DM﹣OD=![]() =
=![]() ,∴点M坐标为(
,∴点M坐标为(![]() ,0).
,0).

【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/kg | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/min | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
若鸭的质量为3.2kg时,烤制时间为_____min.