题目内容
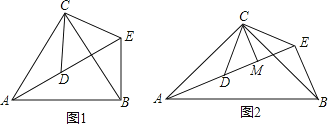
【题目】已知：如图1，
和
均为等边三角形，点A、D、E在同一直线上，连接BE．
求证：
；
求
的度数；
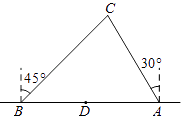
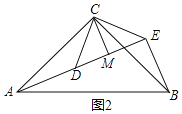
拓展探究：如图2，和均为等腰直角三角形，
，点A、D、E在同一直线上，CM为中DE边上的高，连接BE．
的度数为______
；
探索线段CM、AE、BE之间的数量关系为______
直接写出答案，不需要说明理由
.
【答案】
见解析，
【解析】
由条件
和
均为等边三角形，易证
≌
，从而得到对应边相等，即
；
根据≌，可得
，由点A，D，E在同一直线上，可求出
，从而可以求出
的度数；
首先根据和均为等腰直角三角形，可得
，
，
，据此判断出
；然后根据全等三角形的判定方法，判断出≌，即可判断出
，
，进而判断出的度数为
；
根据
，，
，可得
，所以
，据此判断出
．
解：
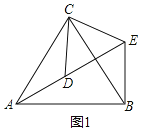
如图1，
和均为等边三角形，
，，
，
．
在和中，
，
≌
，
；
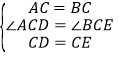如图1，
≌，
，
为等边三角形，
，
点A，D，E在同一直线上，
，
，
；
如图2，和均为等腰直角三角形，
，，，
，
，
即，
在和中，
，
≌，
，，
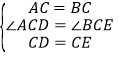点A，D，E在同一直线上，
，
，
，
故答案为：90；
如图2，
，，，
，
，
≌
已证
，
，
，
故答案为：．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
