题目内容
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).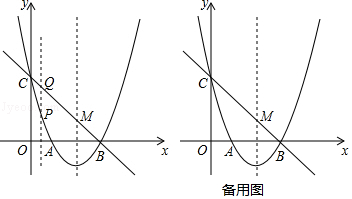
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:把A(1,0),B(3,0),C(0,3)三点代入y=ax2+bx+c,
得 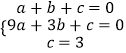 ,解得
,解得 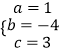 ,
,
则抛物线的解析式为y=x2﹣4x+3;
(2)
解:设直线BC的解析式为y=mx+n,
将点B,C坐标代入y=mx+n,
得 ![]() ,解得
,解得 ![]() ,
,
所以直线BC的解析式为y=﹣x+3.
设P点坐标为(t,t2﹣4t+3),则Q坐标为(t,﹣t+3),
∴PQ=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t=﹣(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,PQ的值最大,最大值为
时,PQ的值最大,最大值为 ![]() ;
;
(3)
解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,
∵点M是对称轴与直线BC的交点,
∴将x=2代入y=﹣x+3,得y=﹣2+3=1,即M(2,1).
∵PQ∥y轴,
∴∠PQB=∠OCB,
∴以M,P,Q为顶点的三角形与△OBC相似包含两种情况:△PMQ∽△OBC或△MPQ∽△OBC.
①当△PMQ∽△OBC时,∠QPM=∠COB=90°,即PM⊥PQ,
∴yP=yM=1,
将yP=1代入y=x2﹣4x+3,得x2﹣4x+3=1,
解得x1=2﹣ ![]() ,x2=2+
,x2=2+ ![]() (舍去),
(舍去),
∴此时P(2﹣ ![]() ,1);
,1);
②当△MPQ∽△OBC时,∠QMP=∠COB=90°,即PM⊥BC,
∴kPM= ![]() =1,
=1,
∴可设直线PM的解析式为y=x+d,
将M(2,1)代入y=x+d,
得2+d=1,解得d=﹣1,
∴y=x﹣1,
解方程组 ![]() ,得
,得 ![]() ,
, ![]() (舍去),
(舍去),
∴此时P(1,0).
综上所述,存在点P,使以点M,P,Q为顶点的三角形与△OBC相似,P点坐标为(2﹣ ![]() ,1)或(1,0).
,1)或(1,0).
【解析】(1)把A(1,0),B(3,0),C(0,3)三点代入y=ax2+bx+c,利用待定系数法求得抛物线的解析式;(2)利用待定系数法求得直线BC的解析式为y=﹣x+3.设P点坐标为(t,t2﹣4t+3),则Q坐标为(t,﹣t+3),那么PQ=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,再利用配方法化为顶点式,即可求出PQ的最大值;(3)由PQ∥y轴,得出∠PQB=∠OCB,那么以M,P,Q为顶点的三角形与△OBC相似包含两种情况:①当△PMQ∽△OBC时,PM⊥PQ,yP=yM=1,易求P(2﹣ ![]() ,1);②当△MPQ∽△OBC时,先求直线PM的解析式,再联立PM与抛物线的解析式,求出P(1,0).
,1);②当△MPQ∽△OBC时,先求直线PM的解析式,再联立PM与抛物线的解析式,求出P(1,0).
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案